< HOME > 5-13-2021 -- America needs "CALCULUS"
https://www.vertex42.com/ExcelTips/unicode-symbols.html
"symbols" "decimal numeric character" reference
How to place "unicode symbols" in your "html" document.
https://en.wikipedia.org/wiki/List_of_XML_and_HTML_character_entity_references
You can enter any Unicode character in an HTML file by
- taking its decimal numeric character reference and adding an ampersand and a hash at the front
and a semi-colon at the end.
For example — should display as an em dash (—). SEE TABLE REFERENCE BELOW. This is the method used in the Unicode test pages.
In the table url CITED below, the "Standard" column indicates the first version of the HTML DTD that defines the character entity reference. To use one of these character entity references in an HTML or XML document, enter an ampersand followed by the entity name and a semicolon, e.g., enter © for the copyright symbol (©).
Alternatively, enter an ampersand, followed by a number sign, a number and a semicolon. For example, to display the copyright symbol ©, enter © (When using this method, use the parenthesized decimal numbers in the third column.) Equivalently, you can enter an ampersand, followed by a number sign, the letter x, a hexadecimal number and a semicolon. For example, to display the copyright symbol © enter © or ©. (When using this method, use the hexadecimal numbers in the third column, without the prefix U+.)
notin, NotElement, notinva ∉ U+2209 (8713) HTML 4.0 (NotElement and notinva added in HTML 5.0) HTMLsymbol ISOtech
not an element of (not in set)
mdash — U+2014 (8212) HTML 4.0 HTMLspecial ISOpub em dash
ne, NotEqual ≠ U+2260 (8800) HTML 4.0 (NotEqual added in HTML 5.0) HTMLsymbol ISOtech not equal to
https://en.wikipedia.org/wiki/List_of_XML_and_HTML_character_entity_references
https://www.rapidtables.com/math/symbols/Basic_Math_Symbols.html
| vertical bar such that A={x|3<x<14}
BBBBBBBBBBBBBBBBBBB
<tr>
<td>notin, NotElement, notinva</td>
<td>∉</td>
<td><a class="mw-redirect" href="/wiki/Mathematical_Operators" title="Mathematical Operators">U+</a>2209 (8713)</td>
<td>HTML 4.0 (NotElement and notinva added in HTML 5.0)</td>
<td>HTMLsymbol</td>
<td>ISOtech</td>
<td>not an element of <i>(not in set)</i></td>
</tr>
BBBBBBBBBBBBBBBBBBBBBBB
https://www.mathsisfun.com/sets/sets-introduction.html
∉ "keyboard" empty set :: https://howtotypeanything.com/type-not-an-element-of/ :: Not An Element Of Symbol [text] in Notepad
○ ○ Alt codes "Notepad"
Chapter 1
"Elementary Set Theory" : https://en.wikipedia.org/wiki/Set_theory
"... Set theory is the branch of "mathematical logic" 1. that studies sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory, as a branch of mathematics, is mostly concerned with those that are relevant to mathematics as a whole.
1. https://en.wikipedia.org/wiki/Mathematical_logic
The modern study of set theory was initiated by the German mathematicians Richard Dedekind and Georg Cantor in the 1870s.
In particular, Georg Cantor is commonly considered the founder of set theory. The non-formalized systems investigated during this early stage go under the name of naive set theory. After the discovery of paradoxes within naive set theory (such as Russell's paradox, Cantor's paradox and Burali-Forti paradox) various axiomatic systems were proposed in the early twentieth century, of which Zermelo–Fraenkel set theory (with or without the axiom of choice) is still the best-known and most studied.
"Set theory" is commonly employed as a foundational system for the whole of mathematics, particularly in the form of Zermelo–Fraenkel set theory with the axiom of choice.
[ https://en.wikipedia.org/wiki/Zermelo%E2%80%93Fraenkel_set_theory ]
[1] Beside its foundational role, set theory also provides the framework to develop a "mathematical theory of infinity", and has various applications in computer science, philosophy and formal semantics.
[ https://plato.stanford.edu/entries/infinity/ ]
Its foundational appeal, together with its paradoxes, its implications for the concept of infinity and its multiple applications, have made set theory an area of major interest for logicians and philosophers of mathematics. Contemporary research into set theory covers a vast array of topics, ranging from the structure of the real number line to the study of the consistency of large cardinals. ..."
https://www.mathsisfun.com/sets/symbols.html
AAAAAAAAAAAAAAAAAAAAAAAAAAA
Mathematical " Set Notation " https://en.wikipedia.org/wiki/Set_(mathematics)
" A set is a gathering together into a whole of definite, distinct objects of our perception or our thought—which are called elements of the set. "
Chapter 1
"Elementary Set Theory" :: https://www.mathsisfun.com/sets/symbols.html
A set can be any collection of objects.
A set of objects can be represented using the notation S = { x | statement about x}
and is read: “S is the set of objects x which make the statement about x true”.
Alternatively, a finite number of objects within S can be denoted by listing the objects and writing
S = {S1, S2, . . ., Sn}
For example, the notation S = { x | x − 4 > 0}
can be used to denote the set of points x "such that" (x-4) is greater than 0.
and the notation T = {A, B, C, D, E}
can be used to represent a set (T) containing the first 5 letters of the alphabet.
A set with no elements is denoted by the symbol ∅ and is known as the empty set.
[ https://www.mathsisfun.com/sets/sets-introduction.html ]
The elements "within" a set are usually selected from some universal set U associated
with the elements x belonging to the set.
When dealing with "real numbers" the universal set U is understood to be the set of all real numbers.
The universal set is usually defined beforehand - or, is implied within the context of how the set is being used.
For example, the universal set U associated with the set T above could be the set of all symbols if that is "appropriate" and within the context of how the set T is being used. [ THIS IS - AT BEST DUBIOUS - BECAUSE IT IS IMPRECISE. ]
The symbol ∈ is read “belongs to” or “is a member of” and the symbol ∉ is read “not in” or “is not a member of”.
The statement x ∈ S is read “x is a member of S ” or “x belongs to S ”.
The statement y ∉ S is read “y does not belong to S” or “y is not a member of S”
The statement x ∈ S is read “x is a member of S ” or “x belongs to S ”.
The statement y ∉ S is read “y does not belong to S” - or “y is not a member of S”.
Let S denote a non-empty set containing real numbers x.
[ https://en.wikipedia.org/wiki/Upper_and_lower_bounds ]
[ https://en.wikipedia.org/wiki/Least-upper-bound_property ]
[ https://en.wikipedia.org/wiki/Infimum_and_supremum ]
This set is said to be "bounded above" if one can find a number b such that for each x ∈ S, one finds x ≤ b.
The number b is called an "upper bound" of the set S.
In a similar fashion, the set S containing real numbers x is said to be "bounded below" if one can find a number k such that k ≤ x for all x ∈ S.
In a similar fashion, the set S containing real numbers x is said to be "bounded below" if one can find a number k such that k ≤ x for all x ∈ S.
The number k is called a lower bound for the set S.
Note that any number greater than b is also an upper bound for S and any number less than k can be considered a lower bound for S.
Let B and C denote the sets
B = { x | x is an upper bound of S} and C = { x | x is a lower bound of S}.
Then the set B has a least upper bound (L.u.b.) and the set C has a greatest lower bound (g.L.b.).
A set which is bounded both above and below is called a bounded set.
[ https://en.wikipedia.org/wiki/Bounded_set ]
[ https://en.wikipedia.org/wiki/List_of_XML_and_HTML_character_entity_references ]
radic, Sqrt √ U+221A (8730) HTML 4.0 (Sqrt added in HTML 5.0) HTMLsymbol ISOtech square root (radical sign)
[ square root :: https://en.wikipedia.org/wiki/Square_root √
"... a number x is a number y such that y2 = x; in other words, a number y whose square (the result of multiplying the number by itself, or y ⋅ y) is x. For example, 4 and −4 are square roots of 16, because 4squared = (−4)squared = 16.
Every nonnegative real number x has a unique nonnegative square root, called the principal square root, which is denoted by √ where the symbol √ is called the radical sign or radix. For example, the principal square root of 9 is 3, because 3squared = 3 ⋅ 3 = 9 and 3 is nonnegative.
The term (or number) whose square root is being considered is known as the radicand.
The radicand is the number or expression underneath the radical sign, in this case 9.
For example, √25 = 5, since 25 = 5 ⋅ 5, or 5 squared.
... Every positive number x has two square roots: +n which is positive, and -n which is negative.
Together, these two roots are denoted as (see ± shorthand). Although the principal square root of a positive number is only one of its two square roots, the designation "the square root" is often used to refer to the principal square root.
For positive x, the "principal square root" can also be written in exponent notation, as x1/2. ...
Square roots of negative numbers can be discussed within the framework of complex numbers.
More generally, square roots can be considered in any context in which a notion of the "square" of a mathematical object is defined. These include "function spaces" and "square matrices", among other mathematical structures. ...
" https://en.wikipedia.org/wiki/Square_root ]
√
Some examples of well known sets are the following:
The set of natural numbers N = {1, 2, 3, . . .}
The set of integers Z = {. . ., −3, −2, −1, 0, 1, 2, 3, . . .}
The set of rational numbers Q = { p/q | p is an integer, q is an integer, q ≠ 0} https://en.wikipedia.org/wiki/Rational_number
The set of prime numbers P = {2, 3, 5, 7, 11, . . .} https://en.wikipedia.org/wiki/Prime_number
The set of complex numbers C = { x + i y | i 2 = −1, x, y are real numbers} https://en.wikipedia.org/wiki/Complex_number
The set of real numbers R = {All decimal numbers} https://en.wikipedia.org/wiki/Real_number
The set of 2-tuples R2 = { (x, y) | x, y are real numbers } https://en.wikipedia.org/wiki/Cartesian_product
The set of 3-tuples R3 = { (x, y, z) | x, y, z are real numbers } https://www.math.brown.edu/tbanchof/Beyond3d/chapter8/section01.html
The set of n-tuples Rn = { (ξ1, ξ2, . . ., ξn) | ξ1, ξ2, . . ., ξn are real numbers } [ https://en.wikipedia.org/wiki/Tuple ]
where it is understood that i is an imaginary unit with the property i2 = −1 and https://en.wikipedia.org/wiki/Imaginary_unit
decimal numbers represent all terminating and nonterminating decimals.
[ https://scholar.flatworldknowledge.com/books/128/fwk-redden-ch01_s01/preview ]
Example 1-1. Intervals [ https://en.wikipedia.org/wiki/Interval_(mathematics) ]
When dealing with real numbers a, b, x it is customary to use the following notations to represent various intervals of real numbers.
Set Notation Set Definition Name
[a, b] {x | a ≤ x ≤ b} closed interval https://www.mathsisfun.com/definitions/closed-interval.html
(a, b) {x | a < x < b} open interval
[a, b) {x | a ≤ x < b} left-closed, right-open
(a, b] {x | a < x ≤ b} left-open, right-closed
(a,∞) {x | x > a} left-open, unbounded
[a,∞) {x | x ≥ a} left-closed,unbounded
(−∞, a) {x | x < a} unbounded, right-open
(−∞, a] {x | x ≤ a} unbounded, right-closed
(−∞,∞) R = {x | −∞ < x < ∞} Set of real numbers
Subsets:
If for every element x ∈ A one can show that x is also an element of a set B, then the set A is called a subset of B or one can say the set A is contained in the set B.
This is expressed using the mathematical statement A ⊂ B, which is read “A is a subset of B ”.
This can also be expressed by saying that "B contains A", which is written as B ⊃ A.
If one can find one element of A which is not in the set B, then A is not a subset of B.
This is expressed using either of the notations A ⊂� B or B ⊃� A.
Note that the above definition implies that every set is a subset of itself, since the elements of a set A belong to the set A.
Whenever A ⊂ B and A ≠ B,
then A is called a proper subset of B.
Set Operations:
Given two sets A and B, the union of these sets is written A ∪ B and defined A ∪ B = { x | x ∈ A or x ∈ B, or x ∈ both A and B}
The intersection of two sets A and B is written A ∩ B and defined A ∩ B = { x | x ∈ both A and B }
If A ∩ B is the empty set, one writes A ∩ B = ∅ and then the sets A and B are said to be disjoint.
The difference between two sets A and B is written A − B and defined A − B = { x | x ∈ A and x /∈ B }
The equality of two sets is written A = B and defined A = B if and only if A ⊂ B and B ⊂ A
That is, if A ⊂ B and B ⊂ A, then the sets A and B must have the same elements which implies equality.
Conversely, if two sets are equal A = B, then A ⊂ B and B ⊂ A since every set is a subset of itself.
A ∪ B A ∩ B A − B
Ac A ∪ (B ∩ C) (A ∪ B)c
Figure 1-1. Selected Venn diagrams.
The complement of set A with respect to the universal set U is written Ac and defined
Ac = { x | x ∈ U but x /∈ A }
Observe that the complement of a set A satisfies the complement laws
A ∪ Ac = U, A ∩ Ac = ∅, ∅c = U, Uc = ∅
The operations of union ∪ and intersection ∩ satisfy the distributive laws
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
1. The difference between two sets A and B in some texts is expressed using the notation A \ B.
and the identity laws
A ∪ ∅ = A, A ∪ U = U, A ∩ U = A, A ∩ ∅ = ∅
The above set operations can be illustrated using circles and rectangles, where
the universal set is denoted by the rectangle and individual sets are denoted by
circles. This pictorial representation for the various set operations was devised by
John Venn2 and are known as Venn diagrams.
Selected Venn diagrams are illustrated in the figure 1-1.
Example 1-2. Equivalent Statements
Prove that the following statements are equivalent A ⊂ B and A ∩ B = A
Solution: To show these statements are equivalent one must show
(i) if A ⊂ B, then A ∩ B = A and (ii) if A ∩ B = A, then it follows that A ⊂ B.
(i) Assume A ⊂ B, then if x ∈ A it follows that x ∈ B since A is a subset of B.
Consequently, one can state that x ∈ (A ∩ B), all of which implies A ⊂ (A ∩ B).
Conversely, if x ∈ (A ∩ B), then x belongs to both A and B and certainly one can
say that x ∈ A. This implies (A ∩ B) ⊂ A. If A ⊂ (A ∩ B) and (A ∩ B) ⊂ A, then it
follows that (A ∩ B) = A.
(ii) Assume A ∩ B = A, then if x ∈ A, it must also be in A ∩ B so that one can say
x ∈ A and x ∈ B, which implies A ⊂ B.
Coordinate Systems
There are many different kinds of coordinate systems - most of which are created to transform a problem or object into a simpler representation.
The rectangular coordinate system with axes labeled x and y provides a way of plotting number
pairs (x, y) which are interpreted as points within a plane.
notes:
2 John Venn (1834-1923) An English mathematician who studied logic and set theory.
3 Also called a cartesian coordinate system and named for Ren´e Descartes (1596-1650)
a French philosopher who applied algebra to geometry problems.
rectangular coordinates polar coordinates
x2 + y2 = ρ2 x = r cos θ,
tan θ = y
x
y = r sin θ
x2 + y2 = r
r = ρ
Figure 1-2. Rectangular and polar coordinate systems
A cartesian or rectangular coordinate system is constructed by selecting two
straight lines intersecting at right angles and labeling the point of intersection as
the origin of the coordinate system and then labeling the horizontal line as the
x-axis and the vertical line as the y-axis. On these axes some kind of a scale is
constructed with positive numbers to the right on the horizontal axis and upward
on the vertical axes. For example, by constructing lines at equally spaced distances
along the axes one can create a grid of intersecting lines.
A point in the plane defined by the two axes can then be represented by a number
pair (x, y).
In rectangular coordinates a number pair (x, y) is said to have the abscissa
x and the ordinate y.
The point (x, y) is located a distance r = �x2 + y2 from the
origin with x representing distance of the point from the y-axis and y representing
the distance of the point from the x-axis. The x axis or abscissa axis and the y axis
or ordinate axis divides the plane into four quadrants labeled I, II, III and IV .
To construct a "polar coordinate system" - one selects an origin for the polar coordinates and labels it 0.
Next, construct a "half-line" similar to the x-axis of threctangular coordinates.
This "half-line" is called the "polar axis" or "initial ray" and the origin is called the pole of the polar coordinate system.
By placing another line on top of the polar axis and rotating this line about the pole through a positive angle θ, measured in radians, one can create a ray emanating from the origin at an angle θ as illustrated in the figure 1-3.
In polar coordinates the rays are illustrated emanating from the origin at equally spaced angular distances around the origin and then
concentric circles are constructed representing constant distances from the origin.
A point in "polar coordinates" is then denoted by the number pair (r, θ) where θ is the angle of rotation associated with the ray and r is a distance outward from the origin along the ray.
The polar origin or pole has the coordinates (0, θ) for any angle
θ. All points having the polar coordinates (ρ, 0), with ρ ≥ 0, lie on the polar axis.
Figure 1-3.
Construction of polar axes
Here, "angle rotations" are treated the same as in trigonometry with a counterclockwise rotation being in the positive direction and a
clockwise rotation being in the negative direction.
Note, that the polar representationof a point is not unique since the angle θ can be increased or decreased by some multiple
of 2π to arrive at the same point.
That is, (r, θ) = (r, θ ± 2nπ) where n is an integer.
Also note, that a ray at angle θ can be extended to represent negative distances along the ray. Points (−r, θ) can also be represented by the number pair (r, θ + π).
Alternatively, one can think of a rectangular point (x, y) and the corresponding polar
point (r, θ) as being related by the equations:
θ = arctan (y/x),
r = √ x2 + y2,
x =r cos θ
y =r sin θ
formula equation (1.1)
An example of a rectangular coordinate system and polar coordinate system are illustrated in the figure 1-2.
Distance Between Two Points in the Plane
Figure 1-4. Distance between points in polar coordinates.
If two points are given in polar coordinates as (r1, θ1) and (r2, θ2), as illustrated in the fig�ure 1-4 - then, one can use the law of cosines
to calculate the distance d between the points - since:
d2 = r 2/1 + r2/2 − 2r1r2 cos(θ1 − θ2)
equation (1.2)
Alternatively, let (x1, y1) and (x2, y2) denote two points which are plotted on a cartesian set of axes as illustrated in the figure 1-5.
The Greek letter ∆ (delta) is used to denote a change in a quantity.
For example, in moving from the point (x1, y1) to the point (x2, y2) the change in x is denoted ∆x = x2 − x1 and the change in y is
denoted ∆y = y2 − y1.
These changes can be thought of as the legs of a right-triangle as illustrated in the figure 1-5.
Figure 1-5.
Using a right-triangle to calculate distance between two points in rectangular coordinates.
The figure 1-5 illustrates that by using the "Pythagorean theorem" the distance d between the two points can be determined from the equations.
d2 = (∆x)2 + (∆y)2 or d = √ (x2 − x1)2 + (y2 − y1)2 (1.3)
Why "counter clockwise" in math? Quadrant numbering
https://www.reddit.com/r/math/comments/3mtyqn/why_are_quadrants_in_a_2_dimensional_graph/
- Angles are measured counterclockwise from the positive x axis.
( http://mathsfirst.massey.ac.nz/Trig/DegRad.htm )
- i think it's because we count like we read in the west, left to right, and then when we stuck another axis on the paper we decided that positive numbers should go "up" instead of down. at that point we were looking at a counterclockwise motion going from the positive x to the positive y
Graphs and Functions
"Math as a tool" > https://asiasociety.org/ ::
https://odu.edu/math/directory
"John H. Heinbockel" > http://www.math.odu.edu/~jhh/jhh
"... OLD DOMINION UNIVERSITY COLLEGE OF SCIENCES DEPARTMENT OF MATHEMATICS AND STATISTICS
John H. Heinbockel > Professor Emeritus
Department of Mathematics and Statistics
Old Dominion University
Norfolk, Virginia 23529 --- E-Mail: jhh@math.odu.edu
http://www.math.odu.edu/~jhh/counter2.html < Professor's Main Page - teXts. etc.
For Free Geometry Book Click Here > [ www.math.odu.edu/~jhh/counter13.html ]
::Geometry
Chapter 1 Preliminaries . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1
Chapter 2 Basic Geometric Concepts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
Chapter 3 Shapes and properties . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .89
Chapter 4 The Pythagorean Theorem. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .137
Chapter 5 Properties of geometric figures . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 185
Chapter 6 Introduction to Mathematical Fundamentals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 233
Chapter 7 Trigonometry I . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .271
Chapter 8 Trigonometry II . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 315
Chapter 9 More properties of geometric shapes. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 351
Chapter 10 Mathematics and Geometry . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 397
Chapter 11 Solid Geometry I. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .459
Chapter 12 Solid Geometry II. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .505
Chapter 13 Additional Topics. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 545
Appendex A Units of measurement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .594
Index. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 596
Calculus VOLume ... "First" :: Chapters 1, 2, 3, 4 & 5 : [ "Neanderthals" & "Math" ]
Modern humans emerged from Africa - and "inquired": ( because, we could speak )
"Hey, Neanderthal ... I need some one - who can build me - a 'regular polyhedra' -- Do YOU know any one?"
Consider: No "Angie's List" & No InterNET
...  - - https://www.nytimes.com/2020/04/09/science/neanderthals-fiber-string-math.html ...
- - https://www.nytimes.com/2020/04/09/science/neanderthals-fiber-string-math.html ...  ...
...
 MATHEMATICS!
MATHEMATICS!
If those short, hairy bastards can do it ... I can! ...
( https://siobhanroberts.com/early-string-ties-us-to-neanderthals/ ) ...
"... A new study, published today in Scientific Reports, adds another talent: "fiber technology" — and perhaps, by extension, numeracy, because strands of string are combined in pairs and sets to form cord.
[ SOURCE: https://www.nature.com/articles/s41598-020-61839-w "... Examination of photomicrographs revealed 3 bundles of fibres with S-twist which were then plied together with a Z-twist to form a 3-ply cord14. The cord is approximately 6.2 mm in length and approximately 0.5 mm in width (Figs. 3, 4). The morphology of the cord fragment closely resembles replica cords produced in modern materials (see SI Fig. 1). Based on the presence of bordered pits15 with torus-margo membranes which are arranged in parallel lines, the fibres resemble gymnosperm (conifer) and come from the inner bark16,17. The torus is surrounded by a margo that controls the pressure in the conifer water transport system,; this mechanism is a strategy that distinguishes gymnosperm from angiosperm (flowering plants)18,19. Juniper, spruce, cedar, and pine bast have been used archaeologically and historically in the manufacture of cordage and textiles (see Supplemental Information). ...
While it is clear that the cord from Abri du Maras demonstrates Neanderthals’ ability to manufacture cordage, it hints at a much larger fibre technology. Once the production of a twisted, plied cord has been accomplished it is possible to manufacture bags, mats, nets, fabric, baskets, structures, snares, and even watercraft3,4,32. The cord from Abri du Maras consists of fibres derived from the inner bark of gymnosperms, likely conifers. The fibrous layer of the inner bark is referred to as bast and eventually hardens to form bark. In order to make cordage, Neanderthals had extensive knowledge of the growth and seasonality of these trees. Bast fibres are easier to separate from the bark and the underlying wood in early spring as the sap begins to rise. The fibres increase in size and thickness as growth continues. The best times for harvesting bast fibres would be from early spring to early summer. Once bark is removed from the tree, beating can help separate the bast fibres from the bark. Additionally, retting the fibres by soaking in water aids in their separation and can soften and improve the quality of the bast. The bast must then be separated into strands and can be twisted into cordage4. In this case, three groups of fibres were separated and twisted clockwise (s-twist). Once twisted the strands were twined counterclockwise (Z-twist) to form a cord.
Ropes and baskets are central to a large number of human activities. They facilitate the transport and storage of foodstuffs, aid in the design of complex tools (hafts, fishing, navigation) or objects (art, decoration).
... The cord fragment from Abri du Maras is the oldest direct evidence of fibre technology to date. Its production demonstrates a detailed ecological understanding of trees and how to transform them into entirely different functional substances. Fibre technology would have been an important part of everyday life and would have influenced seasonal scheduling and mobility. Furthermore, the production of cordage implies a cognitive understanding of numeracy and context sensitive operational memory. Given the ongoing revelations of Neanderthal art and technology2,45,46, it is difficult to see how we can regard Neanderthals as anything other than the cognitive equals of modern humans. ..." ]
“They were not supposed to be doing much of anything, really, if you go with the stereotype,” said Bruce Hardy, a paleoanthropologist at Kenyon College in Ohio, and the paper’s lead author.
... Other scholars during the review process expressed an old-fashioned skepticism that Neanderthals [ or SUSAN ] would engage in behavior as sophisticated as the step-by-step process of "making cord". ...
... The excavated fragment of cord was likely derived from the inner bark of a conifer or evergreen tree, such as a pine or juniper. It was composed of fibers plied together: numerous fibers twisted counterclockwise, in an “S-twist,” to make yarn; and then three strands of yarn twisted in the opposite direction, clockwise with a “Z-twist,” to make cord. The twisting and retwisting produce a tensile strength. ... Although the researchers were careful in speculating about the uses of this fragment, they proposed that lengths of cord could have been combined into larger structures such as bags, mats, nets, fabric, baskets, snares and even boats. ... Moreover, they suggested, “the production of cordage necessitates an understanding of mathematical concepts and general numeracy.” ... “Cordage production entails context sensitive operational memory to keep track of each operation,” they wrote. “As the structure becomes more complex (multiple cords twisted to form a rope, ropes interlaced to form knots), it demonstrates an ‘infinite use of finite means’ and requires a cognitive complexity similar to that required by human language. ... Dr. Hardy noted the cognitive parallels. “I can’t have a sentence without words, and I can’t have words without the individual sounds that carry meaning,” he said. “So I can’t have a rope or a cord or a bag or a net without the other steps along the way. You can’t start with the end product.” It’s a scaffolding process that scales up. ... Some scholars expressed concern that the study was reading too much into, well, a piece of string. ... “Whilst not wanting to belittle the Neanderthal achievement, which does seem much closer to that of Pleistocene Homo sapiens that until recently we gave them credit for, this does not make them cognitive geniuses,” said Paul Pettitt, a Paleolithic archaeologist at Durham University in England. ... He viewed the finding as “a welcome addition to our understanding of the behavioral repertoire of the Neanderthals.” But the interpretation, he said, “fuels the somewhat simplistic debate that polarizes the issue between Neanderthals as being either stupid, or geniuses.” ... Dr. Hardy said, “I’m not saying they are geniuses. I am saying they are not morons.” ... In short, they were not that different from the average Homo sapiens. 'Cognitively, they are us,” Dr. Hardy said. “They’re not us exactly, but they are close enough.' ..."
The regular solids or "regular polyhedra" --- --- are solid geometric figures - with the same identical regular polygon on each face.
--- are solid geometric figures - with the same identical regular polygon on each face.
There are only five regular solids discovered by the ancient Greek mathematicians. [ https://www.famousmathematicians.net/famous-greek-mathematicians/ ] ...
These five solids are the following:
1. the tetrahedron (4 faces)
2. the cube or hexadron (6 faces)
3.the octahedron (8 faces)
4. the dodecahedron (12 faces)
5. the icosahedron (20 faces)
( As of this date - there are not more than these 5 listed : https://math.hmc.edu/funfacts/regular-solids/ )
Each figure ["solid"] follows the "Euler formula" :
Number of faces (F) + Number of vertices (V) = Number of edges (E) + 2 ... F + V = E + 2 ... ( YOU Tube )
COVER: 
Title Page : http://www.math.odu.edu/~jhh/Volume-1.PDF [ 566 PAGES ]
"... Introduction to Calculus : Volume I ::
by J.H. Heinbockel ..." " Professor Emeritus > Old Dominion University" : https://www.odu.edu/facultystaff
http://www.math.odu.edu/~jhh/Volume-2.PDF "... Introduction to Calculus Volume II by J.H. Heinbockel ..."
Preface
... This is the first volume of an introductory calculus presentation intended for future scientists and engineers.
[ Susan - a retired software engineer and technical documentation professional - may be able to understand it.]
Volume I contains five chapters emphasizing "fundamental concepts" from calculus and analytic geometry and the application of these concepts to selected areas of science and engineering.
Chapter one is a review of fundamental background material needed for the development of differential and integral calculus together with an introduction to limits.
The main purpose of these two volumes is to:
(i) Provide an introduction to calculus in its many forms.
(ii) Give some presentations to illustrate how powerful calculus is as a mathematical tool for solving a variety of scientific problems.
(iii) Present numerous examples to show how calculus can be extended to other mathematical areas.
(iv) Provide material "detailed enough" so - that [THESE] two volumes of basic material -can be used as reference books.
(v) Introduce concepts from a variety of application areas, such as biology, chemistry, economics, physics and engineering, to demonstrate applications of calculus.
(vi) Emphasize that "definitions" are extremely important in the study of any mathematical subject. NOT ARBITRARY!
(vii) Introduce proofs of important results as an aid to the development of analytical and critical reasoning skills.
(viii) Introduce mathematical terminology and symbols which can be used to help model physical systems and
(ix) Illustrate multiple approaches to various calculus subjects.
If - the main thrust of an introductory calculus course is the application of calculus to solve problems, then a student must quickly get to a point where he or she understands enough fundamentals so that calculus can be used as a tool for solving the problems of interest.
If - on the other hand, a deeper understanding of calculus is required in order to develop the basics for more advanced mathematical
iii efforts, then students need to be exposed to theorems and proofs.
If - the calculus course leans toward more applications, rather than "theory", then the proofs presented throughout the text can be skimmed over.
However, if the calculus course is for mathematics majors, then one would want to be sure to go into the proofs in greater detail;
- because - these "proofs" are laying the groundwork and providing background material for the study of more advanced concepts.
https://en.wikipedia.org/wiki/Mathematical_proof ...
"... A mathematical proof is an inferential argument for a mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use other previously established statements, such as theorems; but every proof can, in principle, be constructed using only certain basic or original assumptions known as axioms,[2][3][4] along with the accepted rules of inference. Proofs are examples of exhaustive deductive reasoning which establish logical certainty, to be distinguished from empirical arguments or non-exhaustive inductive reasoning which establish "reasonable expectation". Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in all possible cases. An unproven proposition that is believed to be true is known as a conjecture, or a hypothesis if frequently used as an assumption for further mathematical work.[5]
Proofs employ logic expressed in mathematical symbols, along with natural language which usually admits some ambiguity. In most mathematical literature, proofs are written in terms of rigorous informal logic. Purely formal proofs, written fully in symbolic language without the involvement of natural language, are considered in proof theory. The distinction between formal and informal proofs has led to much examination of current and historical mathematical practice, quasi-empiricism in mathematics, and so-called folk mathematics, oral traditions in the mainstream mathematical community or in other cultures. The philosophy of mathematics is concerned with the role of language and logic in proofs, and mathematics as a language. ..."
 If you are a beginner in calculus, then be sure that you have had the appropriate background material of algebra and trigonometry. [ If you are reviewing the subject - like Susan - then, review algebra and trigonometry - also. ]
If you are a beginner in calculus, then be sure that you have had the appropriate background material of algebra and trigonometry. [ If you are reviewing the subject - like Susan - then, review algebra and trigonometry - also. ]
algebra: https://en.wikipedia.org/wiki/Algebra [ https://en.wikipedia.org/wiki/Glossary_of_mathematical_symbols "... In its most general form, algebra is the study of mathematical symbols and the rules for manipulating these symbols;[3] it [Algebra] is a unifying thread of almost all of mathematics.[4] It [Algebra] includes everything from elementary equation solving to the study of "abstractions" such as groups, rings, and fields. The more basic parts of algebra are called elementary algebra; the more abstract parts are called abstract algebra or modern algebra. Elementary algebra is generally considered to be essential for any study of mathematics, science, or engineering, as well as such applications as medicine and economics. Abstract algebra is a major area in advanced mathematics, studied primarily by professional mathematicians. ..."
trigonometry: https://en.wikipedia.org/wiki/Trigonometry
"... Trigonometry (from Greek trigōnon, "triangle" and metron, "measure"[1]) is a branch of mathematics that studies relationships between side lengths and angles of triangles.
... The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies.[2] ...The Greeks focused on the calculation of chords, [See Neanderthals above] - while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions) such as sine.[3] Throughout history, trigonometry has been applied in areas such as geodesy, surveying, celestial mechanics, and navigation.[4] Trigonometry is known for its many identities. These trigonometric identities[5][6] are commonly used for rewriting trigonometrical expressions with the aim to simplify an expression, to find a more useful form of an expression, or to solve an equation.[7] ..."
If you don’t understand something - then, don’t be afraid to ask your instructor a question.
[ If your "instructor" is grumpy - or ignorant - then, ask the smartest kid in the room; And if, the "smartest kid in the room" is different than you - appreciate the diversity - of your situation; For example, Susan grew up in "inner city" Columbus, Ohio [1954-1972 ]. The "smartest kids" - in Susan's public school classes - were often African Americans - and, other "minorities" ... Susan was told she was "white". Thus, when Susan got to "Silicon Valley" California (circa 1999) - she excelled - at working with very smart people - many - who were not "white" - from all over the world. ]
Go to the library and check out some other calculus books to get a presentation of the subject from a different perspective.:: The internet is a place where one can find numerous help aids for calculus. Also, on the internet - one can find many illustrations of the applications of calculus.
applications of calculus: https://allusesof.com/math/51-amazing-uses-of-calculus-in-real-life/
These additional study aids will show you that there are multiple approaches to various calculus subjects and should help you with the development of your analytical and reasoning skills. - J.H. Heinbockel - September 2012
Table of Contents : "Introduction to Calculus : Volume I"
Chapter 2 Differential Calculus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
Slope of Tangent Line to Curve, The Derivative of y = f(x), Right and Left-hand
Derivatives, Alternative Notations for the Derivative, Higher Derivatives, Rules and
Properties, Differentiation of a Composite Function, Differentials, Differentiation
of Implicit Functions, Importance of Tangent Line and Derivative Function f0(x),
Rolle’s Theorem, The Mean-Value Theorem, Cauchy’s Generalized Mean-Value The�orem, Derivative of the Logarithm Function, Derivative of the Exponential Function,
Derivative and Continuity, Maxima and Minima, Concavity of Curve, Comments on
Local Maxima and Minima, First Derivative Test, Second Derivative Test, Loga�rithmic Differentiation, Differentiation of Inverse Functions, Differentiation of Para�metric Equations, Differentiation of the Trigonometric Functions, Simple Harmonic
Motion, L´Hˆopital’s Rule, Differentiation of Inverse Trigonometric Functions, Hyper�bolic Functions and their Derivatives, Approximations, Hyperbolic Identities, Euler’s
Formula, Derivatives of the Hyperbolic Functions, Inverse Hyperbolic Functions and
their Derivatives, Relations between Inverse Hyperbolic Functions, Derivatives of the
Inverse Hyperbolic Functions, Table of Derivatives, Table of Differentials, Partial
Derivatives, Total Differential, Notation, Differential Operator, Maxima and Minima
for Functions of Two Variables, Implicit Differentiation
Chapter 3 Integral Calculus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 175
Summations, Special Sums, Integration, Properties of the Integral Operator, Notation,
Integration of derivatives, Polynomials, General Considerations, Table of Integrals,
Trigonometric Substitutions, Products of Sines and Cosines, Special Trigonometric
Integrals, Method of Partial Fractions, Sums and Differences of Squares, Summary of
Integrals, Reduction Formula, The Definite Integral, Fundamental theorem of integral
calculus, Properties of the Definite Integral, Solids of Revolution, Slicing Method,
Integration by Parts, Physical Interpretation, Improper Integrals, Integrals used to
define Functions, Arc Length, Area Polar Coordinates, Arc Length in Polar Coordi�nates, Surface of Revolution, Mean Value Theorems for Integrals, Proof of Mean Value
Theorems, Differentiation of Integrals, Double Integrals, Summations over nonrect�angular regions, Polar Coordinates, Cylindrical Coordinates, Spherical Coordinates,
Using Table of Integrals, The Bliss Theorem
Chapter 4 Sequences, Summations and Products . . . . . . . . . . . . .271
Sequences, Limit of a Sequence, Convergence of a sequence, Divergence of a sequence,
Relation between Sequences and Functions, Establish Bounds for Sequences, Addi�tional Terminology Associated with Sequences, Stolz -Ces`aro Theorem, Examples of
Sequences, Infinite Series, Sequence of Partial Sums, Convergence and Divergence of
a Series, Comparison of Two Series, Test For Divergence, Cauchy Convergence, The
Integral Test for Convergence, Alternating Series Test, Bracketing Terms of a Con�vergent Series, Comparison Tests, Ratio Comparison Test, Absolute Convergence,
Slowly Converging or Slowly Diverging Series, Certain Limits, Power Series, Opera�tions with Power Series, Maclaurin Series, Taylor and Maclaurin Series, Taylor Series
for Functions of Two Variables, Alternative Derivation of the Taylor Series, Remain�der Term for Taylor Series, Schl¨omilch and Roche remainder term, Indeterminate
forms 0 · ∞, ∞ − ∞, 00, ∞0, 1∞ , Modification of a Series, Conditional Convergence, Algebraic Operations with Series, Bernoulli Numbers, Euler Numbers, Functions De�fined by Series, Generating Functions, Functions Defined by Products, Continued Fractions, Terminology, Evaluation of Continued Fractions, Convergent Continued Fraction, Regular Continued Fractions, Euler’s Theorem for Continued Fractions,
Gauss Representation for the Hypergeometric Function, Representation of Functions, Fourier Series, Properties of the Fourier trigonometric series, Fourier Series of Odd Functions, Fourier Series of Even Functions, Options,
Chapter 5 Applications of Calculus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .363
Related Rates, Newton’s Laws, Newton’s Law of Gravitation, Work, Energy, First
Moments and Center of Gravity, Centroid and Center of Mass, Centroid of an Area,
Symmetry, Centroids of composite shapes, Centroid for Curve, Higher Order Mo�ments, Moment of Inertia of an Area, Moment of Inertia of a Solid, Moment of Inertia
of Composite Shapes, Pressure, Chemical Kinetics, Rates of Reactions, The Law of
Mass Action, Differential Equations, Spring-mass System, Simple Harmonic Motion,
Damping Forces, Mechanical Resonance, Particular Solution, Torsional Vibrations,
The simple pendulum, Electrical Circuits, Thermodynamics, Radioactive Decay, Eco�nomics, Population Models, Approximations, Partial Differential Equations, Easy to
Solve Partial Differential Equations
Appendix A Units of Measurement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 452
Appendix B Background Material . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .454
( Note that appendix B contains a summary of fundamentals from algebra and trigonometry which is a prerequisite for the study of calculus.)
Appendix C Table of Integrals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 466
Appendix D Solutions to Selected Problems . . . . . . . . . . . . . . . . . . . 520
Index . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .552
[ SOURCE: http://mathandmultimedia.com/2011/05/28/platonic-solids/ "There Are Only Five Platonic Solids"
Interestingly, even though we can create infinitely many regular polygons, there are only five regular polyhedra. And the proof is fairly easy. Before we discuss the proof, let us familiarize ourselves with the different terms which we will use in the proof.
In the following discussion, vertex will refer to the corner of a Platonic solid, face will refer to the regular polygons that make up the solid, and side (edges in 3D) will refer the side of the polygon.
The Proof:
Let 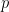 be the number of sides of a regular polygon on a Platonic solid, and
be the number of sides of a regular polygon on a Platonic solid, and  be the number of polygons meeting at each vertex. Let us represent each regular polygon with
be the number of polygons meeting at each vertex. Let us represent each regular polygon with 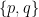 . For example, a cube maybe represented as
. For example, a cube maybe represented as 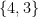 since the faces of a cube (the squares) have four sides, and three squares meet at a cube’s vertex.
since the faces of a cube (the squares) have four sides, and three squares meet at a cube’s vertex.
Notice that the interior angles of the regular polygon can be expressed as 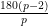 (recall sum of interior angles of a polygon) which is equal to
(recall sum of interior angles of a polygon) which is equal to  . Since
. Since  is convex, the sum of the angles at one vertex is less than 360 degrees (Can you see why?). Therefore, we can setup the following inequality:
is convex, the sum of the angles at one vertex is less than 360 degrees (Can you see why?). Therefore, we can setup the following inequality:


It is clear that the values of  and
and  must be both greater than
must be both greater than 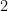 (Why?). Now, if
(Why?). Now, if 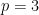 , the only possible values for
, the only possible values for  are
are  and
and 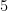 . These values give us the solids
. These values give us the solids 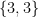 (the tetrahedron),
(the tetrahedron), 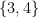 (the octahedron) and
(the octahedron) and  (the icosahedron). If
(the icosahedron). If  , we only have
, we only have  , (the cube). If
, (the cube). If 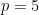 , then, we have only
, then, we have only  , (the dodecahedron). Now,
, (the dodecahedron). Now, cannot be greater than
cannot be greater than  since it will not satisfy the inequality.
since it will not satisfy the inequality.
Therefore, the only platonic solids are 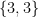 ,
, 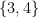 ,
,  ,
, 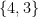 and
and  . Hence, there are only five platonic solids, and we are done with our proof.
. Hence, there are only five platonic solids, and we are done with our proof.
SOURCE: https://en.wikipedia.org/wiki/Platonic_solid :: https://en.wikipedia.org/wiki/Polyhedron
The regular solids or "regular polyhedral" are solid geometric figures with the same identical regular polygon on each face.
There are only five regular solids discovered by the ancient Greek mathematicians.
These five solids are the following.
 tetrahedron
tetrahedron 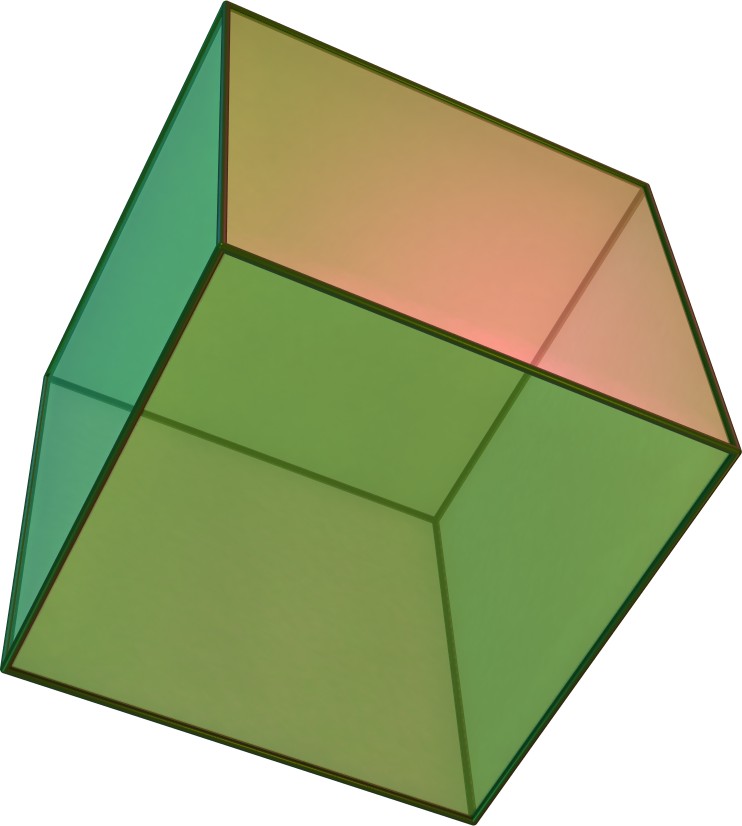 hexadron
hexadron  octahedron
octahedron  dodecahedron
dodecahedron  icosahedron
icosahedron
hhh [ https://es.wikipedia.org/wiki/Arquitectura < GREEKS ]
the tetrahedron (4 faces)
the cube or hexadron (6 faces)
the octahedron (8 faces)
the dodecahedron (12 faces)
the icosahedron (20 faces) :: https://mathworld.wolfram.com/Icosahedron.html
< https://en.wikipedia.org/wiki/Euler's_formula
Each figure follows the Euler formula / Euler Characteristic ::
Number of faces (F) + Number of vertices (V) = Number of edges (E) + 2 :: F + V = E + 2
Euler Characteristic :: https://en.wikipedia.org/wiki/Euler_characteristic
"... In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent. It is commonly denoted by {\displaystyle \chi } (Greek lower-case letter chi).
(Greek lower-case letter chi).
The Euler characteristic was originally defined for polyhedra and used to prove various theorems about them, including the classification of the Platonic solids. It was stated for Platonic solids in 1537 in an unpublished manuscript by Francesco Maurolico.[1] Leonhard Euler, for whom the concept is named, introduced it for convex polyhedra more generally but failed to rigorously prove that it is an invariant. In modern mathematics, the Euler characteristic arises from homology and, more abstractly, homological algebra. ..."
(mathematical constant)
 < https://en.wikipedia.org/wiki/Category:E_(mathematical_constant) :: Category:e (mathematical constant)
< https://en.wikipedia.org/wiki/Category:E_(mathematical_constant) :: Category:e (mathematical constant)
SOURCE: https://en.wikipedia.org/wiki/Euler%27s_formula
"... Euler's formula, named after Leonhard Euler 1 , is a mathematical2 formula3 in complex analysis4 that establishes the fundamental relationship between the trigonometric functions5 and the complex exponential function6.
Euler's formula7 states that for any real number 8 x:
- {\displaystyle e^{ix}=\cos x+i\sin x,}

where e9 is the base of the natural logarithm, i is the imaginary unit 10, and cos and sin are the trigonometric functions 11 cosine12 and sine13 respectively.
This complex exponential function14 is sometimes denoted cis x ("cosine plus i sine").
The formula is still valid if x is a complex number, and so some authors refer to the more general complex version as Euler's formula.[1 ] 15
Euler's formula is ubiquitous in mathematics, physics, and engineering. The physicist Richard Feynman 16 called the equation "our jewel" and "the most remarkable formula in mathematics".[2] 17
When x = π, Euler's formula evaluates to eiπ + 1 = 0, which is known as Euler's identity. 18 ..."
9. https://en.wikipedia.org/wiki/E_(mathematical_constant)
14. https://en.wikipedia.org/wiki/Exponential_function
The selected applications come mainly from the areas of economics, physics, biology, chemistry and engineering.
[ GREEK ARCHITECTURE ]  < PARTHENON > https://en.wikipedia.org/wiki/Parthenon
< PARTHENON > https://en.wikipedia.org/wiki/Parthenon
( https://www.amazon.com/Helix-Oxford-Maths-Set-B43000/dp/B000J66XPG )
Chapter 1 "...Chapter one is a review of fundamental background material needed for the development of differential and integral calculus together with an introduction to limits. ..."
"differential calculus" : ... a subfield of calculus that studies the rates at which quantities change.
"integral calculus" : ... a subfield of calculus [that] concerns accumulation of quantities, and areas under or between curves.
https://en.wikipedia.org/wiki/Limit_(mathematics)
"limits" : In mathematics, a limit is the value that a function 1. (or sequence 2.) approaches as the input (or index 3.) approaches some value.
Limits are essential to calculus and mathematical analysis, 4. and are used to define continuity 5., derivatives 6., and integrals 7..
The concept of a limit of a sequence i8. s further generalized to the concept of a limit of a topological net, 9.
and is closely related to limit 10. and direct limit 11. in category theory. 12.
In formulas, a limit of a function is usually written as: 
and is read as "the limit of f of x as x approaches c equals L".
The fact that a function f approaches the limit L as x approaches c is sometimes denoted by a right arrow (→ )or
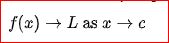 ... which reads "f of x tends to L as x tends to c".
... which reads "f of x tends to L as x tends to c".
Sets, Functions, Graphs and Limits
????? The study of different types of functions, limits associated with these [types of] functions and how these functions change, (together with the ability to graphically illustrate basic concepts associated with these functions), is fundamental to the understanding of calculus. ????
[ The ability to write a text book - for an American audience - requires the ability to speak American English.]
These important issues [ x,y,z ...] are presented along with the development of some additional elementary concepts which will aid in our later studies of more advanced concepts.
In this chapter [Chapter 1] and throughout this text be aware that definitions [and their consequences] are the keys to success for the understanding of calculus and its many applications and extensions.
[ SOURCE: https://scholars.unh.edu/cgi/viewcontent.cgi?article=1116&context=honors ]
Note that appendix B contains a summary of fundamentals from algebra and trigonometry which is [are] a prerequisiteS for the study of calculus.
This first chapter is a preliminary to calculus and begins by introducing the concepts of a function, graph of a function and limits associated with functions.
These concepts are "introduced" - using some basic elements from the theory of sets.
http://pages.stat.wisc.edu/~ifischer/calculus.pdf : < BASIC CALCULUS REFRESHER by Ismor Fischer, Ph.D. Dept. of Statistics UW-Madison
Elementary Set Theory
[ https://www.amherst.edu/system/files/media/0397/logicsetsproof.pdf ]
[ http://www.math.lsa.umich.edu/~kesmith/295handout1-2010.pdf ]
A set can be any collection of objects. A set of objects can be represented using the notation
"set notation" mathematics : Set notation is used in mathematics to essentially list numbers, objects or outcomes.
Set notation uses curly brackets { } which are sometimes referred to as braces. Objects placed within the brackets are called the elements of a set, and do not have to be in any specific order.
"elements of a set" mathematics https://en.wikipedia.org/wiki/Element_(mathematics)
S = { x | statement about x} ( keyboard symbol "vertical bar" )
SOURCE: https://en.wikipedia.org/wiki/Vertical_bar )
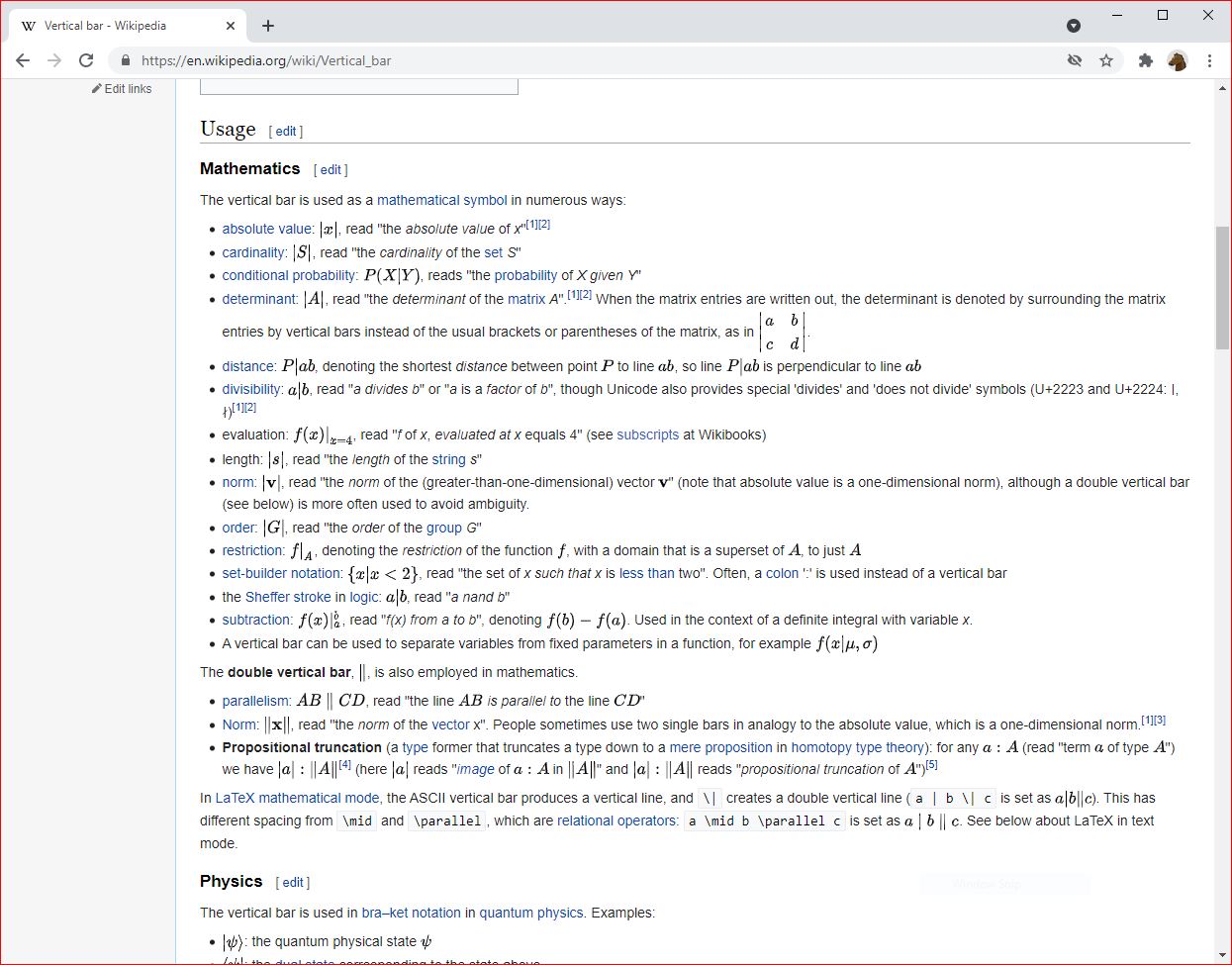
"... Mathematics
The vertical bar is used as a mathematical symbol in numerous ways: [ also see image above ]
- absolute value: {\displaystyle |x|}
 , read "the absolute value of x"[1][2]
, read "the absolute value of x"[1][2]
- cardinality: {\displaystyle |S|}
 , read "the cardinality of the set S"
, read "the cardinality of the set S"
- conditional probability: {\displaystyle P(X|Y)}
 , reads "the probability of X given Y"
, reads "the probability of X given Y"
- determinant: {\displaystyle |A|}
 , read "the determinant of the matrix A".[1][2] When the matrix entries are written out, the determinant is denoted by surrounding the matrix entries by vertical bars instead of the usual brackets or parentheses of the matrix, as in {\displaystyle {\begin{vmatrix}a&b\\c&d\end{vmatrix}}}
, read "the determinant of the matrix A".[1][2] When the matrix entries are written out, the determinant is denoted by surrounding the matrix entries by vertical bars instead of the usual brackets or parentheses of the matrix, as in {\displaystyle {\begin{vmatrix}a&b\\c&d\end{vmatrix}}} .
.
- distance: {\displaystyle P|ab}
 , denoting the shortest distance between point {\displaystyle P}
, denoting the shortest distance between point {\displaystyle P} to line {\displaystyle ab}
to line {\displaystyle ab} , so line {\displaystyle P|ab}
, so line {\displaystyle P|ab} is perpendicular to line {\displaystyle ab}
is perpendicular to line {\displaystyle ab}
- divisibility: {\displaystyle a|b}
 , read "a divides b" or "a is a factor of b", though Unicode also provides special 'divides' and 'does not divide' symbols (U+2223 and U+2224: ∣, ∤)[1][2]
, read "a divides b" or "a is a factor of b", though Unicode also provides special 'divides' and 'does not divide' symbols (U+2223 and U+2224: ∣, ∤)[1][2]
- evaluation: {\displaystyle f(x)|_{x=4}}
 , read "f of x, evaluated at x equals 4" (see subscripts at Wikibooks)
, read "f of x, evaluated at x equals 4" (see subscripts at Wikibooks)
- length: {\displaystyle |s|}
 , read "the length of the string s"
, read "the length of the string s"
- norm: {\displaystyle |\mathbf {v} |}
 , read "the norm of the (greater-than-one-dimensional) vector {\displaystyle \mathbf {v} }
, read "the norm of the (greater-than-one-dimensional) vector {\displaystyle \mathbf {v} } " (note that absolute value is a one-dimensional norm), although a double vertical bar (see below) is more often used to avoid ambiguity.
" (note that absolute value is a one-dimensional norm), although a double vertical bar (see below) is more often used to avoid ambiguity.
- order: {\displaystyle |G|}
 , read "the order of the group G"
, read "the order of the group G"
- restriction: {\displaystyle f|_{A}}
 , denoting the restriction of the function {\displaystyle f}
, denoting the restriction of the function {\displaystyle f} , with a domain that is a superset of {\displaystyle A}
, with a domain that is a superset of {\displaystyle A} , to just {\displaystyle A}
, to just {\displaystyle A}
- set-builder notation: {\displaystyle \{x|x<2\}}
 , read "the set of x such that x is less than two". Often, a colon ':' is used instead of a vertical bar
, read "the set of x such that x is less than two". Often, a colon ':' is used instead of a vertical bar
- the Sheffer stroke in logic: {\displaystyle a|b}
 , read "a nand b"
, read "a nand b"
- subtraction: {\displaystyle f(x)\vert _{a}^{b}}
 , read "f(x) from a to b", denoting {\displaystyle f(b)-f(a)}
, read "f(x) from a to b", denoting {\displaystyle f(b)-f(a)} . Used in the context of a definite integral with variable x.
. Used in the context of a definite integral with variable x.
- A vertical bar can be used to separate variables from fixed parameters in a function, for example {\displaystyle f(x|\mu ,\sigma )}

The double vertical bar, {\displaystyle \|} , is also employed in mathematics.
, is also employed in mathematics.
- parallelism: {\displaystyle AB\parallel CD}
 , read "the line {\displaystyle AB}
, read "the line {\displaystyle AB} is parallel to the line {\displaystyle CD}
is parallel to the line {\displaystyle CD} "
"
- Norm: {\displaystyle \|\mathbf {x} \|}
 , read "the norm of the vector x". People sometimes use two single bars in analogy to the absolute value, which is a one-dimensional norm.[1][3]
, read "the norm of the vector x". People sometimes use two single bars in analogy to the absolute value, which is a one-dimensional norm.[1][3]
- Propositional truncation (a type former that truncates a type down to a mere proposition in homotopy type theory): for any {\displaystyle a:A}
 (read "term {\displaystyle a}
(read "term {\displaystyle a} of type {\displaystyle A}
of type {\displaystyle A} ") we have {\displaystyle |a|:\left\|A\right\|}
") we have {\displaystyle |a|:\left\|A\right\|} [4] (here {\displaystyle |a|}
[4] (here {\displaystyle |a|} reads "image of {\displaystyle a:A}
reads "image of {\displaystyle a:A} in {\displaystyle \left\|A\right\|}
in {\displaystyle \left\|A\right\|} " and {\displaystyle |a|:\left\|A\right\|}
" and {\displaystyle |a|:\left\|A\right\|} reads "propositional truncation of {\displaystyle A}
reads "propositional truncation of {\displaystyle A} ")[5]
")[5]
In LaTeX mathematical mode, the ASCII vertical bar produces a vertical line, and \| creates a double vertical line (a | b \| c is set as {\displaystyle a|b\|c} ). This has different spacing from
). This has different spacing from \mid and \parallel, which are relational operators: a \mid b \parallel c is set as {\displaystyle a\mid b\parallel c} . See below about LaTeX in text mode. ..."
. See below about LaTeX in text mode. ..."
"S equals the set of objects x which make the statement about x true"
and is read aloud, “S is the set of objects x which make the statement about x true”.
Alternatively, a finite number of objects within S can be denoted by listing the objects and writing
S = {S1, S2, . . ., Sn}
For example, the notation S = { x | x − 4 > 0}
can be used to denote the set [S] of points "x" which are greater than 4
and the notation T = {A, B, C, D, E} can be used to represent a set [T] containing the first 5 letters of the alphabet.
A set with no elements is denoted by the symbol ∅ and is known as the "empty set".
The "elements" -within a set - are usually selected from some "universal set" U associated
with the elements x belonging to the set.
When dealing with "real numbers" the universal set U is understood to be the set of all real numbers.
The universal set is usually defined beforehand or is implied within the context of how the set is being used.
For example, the universal set - associated with the set T above - could be the "set of all symbols" - if that is appropriate and within the context of how the set T is being used.
[ "set of all symbols" : alphabet > https://en.wikipedia.org/wiki/Alphabet : "American Alphabet" ( https://en.wikipedia.org/wiki/Latin_alphabet )
The symbol ∈ is read “belongs to” or “is a member of” and the symbol ∈/ is read “not in” or “is not a member of”.
The statement x ∈ S is read “x is a member of S ” or “x belongs to S ”.
The statement y /∈ S is read “y does not belong to S” or “y is not a member of S”.
MATHEMATICAL SYMBOLS : ∌ ∌
SOURCE: https://support.microsoft.com/en-us/office/insert-mathematical-symbols-91a4b04c-84a8-4de9-bd13-8609e14bed58
Insert mathematical symbols : Word for Microsoft 365 Word 2019 Word 2016 Word 2013 Word 2010 Word 2007
In Word, you can insert mathematical symbols into equations or text by using the equation tools.
-
On the Insert tab, in the Symbols group, click the arrow under Equation, and then click Insert New Equation.
 HHHHHHHHHHHH
HHHHHHHHHHHH
-
Under Equation Tools, on the Design tab, in the Symbols group, click the More arrow.
-
Click the arrow next to the name of the symbol set, and then select the symbol set that you want to display.
-
Click the symbol that you want to insert.
Available symbol sets:
The following mathematical symbol sets are available in the Symbols group in Word. After clicking the More arrow, click the menu at the top of the symbols list to see each grouping of symbols.
|
Symbol set
|
Subset
|
Definition
|
|
Basic Math
|
None
|
Commonly used mathematical symbols, such as > and <
|
|
Greek Letters
|
Lowercase
|
Lowercase letters from the Greek alphabet
|
|
Uppercase
|
Uppercase letters from the Greek alphabet
|
|
Letter-Like Symbols
|
None
|
Symbols that resemble letters
|
|
Operators
|
Common Binary Operators
|
Symbols that act on two quantities, such as + and ÷
|
|
Common Relational Operators
|
Symbols that express a relationship between two expressions, such as = and ~
|
|
Basic N-ary Operators
|
Operators that act across a range of variables or terms
|
|
Advanced Binary Operators
|
Additional symbols that act on two quantities
|
|
Advanced Relational Operators
|
Additional symbols that express a relationship between two expressions
|
|
Arrows
|
None
|
Symbols that indicate direction
|
|
Negated Relations
|
None
|
Symbols that express a negated relationship
|
|
Scripts
|
Scripts
|
The mathematical Script typeface
|
|
Frakturs
|
The mathematical Fraktur typeface
https://en.wikipedia.org/wiki/Fraktur_(folk_art)
|
|
Double-Struck
|
The mathematical double-struck typeface
|
|
Geometry
|
None
|
Commonly used geometric symbols
|
VIDEO > https://www.youtube.com/watch?v=saOG7Uooeho
Let S denote a non-empty set containing real numbers x.
This set is said to be "bounded above" if one can find a number b such that for each x ∈ S, one finds x ≤ b.
The number b is called an "upper bound" of the set S. In a similar fashion the set S [ https://en.wikipedia.org/wiki/Number ]
containing real numbers x is said to be bounded below if one can find a number
such that ≤ x for all x ∈ S. The number � is called a "lower bound" for the set S.
Note, that any number greater than b is also an upper bound for S and any number
less than can be considered a lower bound for S. Let B and C denote the sets
B = { x | x is an upper bound of S} and C = { x | x is a lower bound of S},
then the set B has a least upper bound (l.u.b.) and the set C has a greatest lower
bound (g.u.b.).
A set which is bounded both above and below is called a "bounded set".
Some examples of well known sets are the following:
The set of natural numbers N = {1, 2, 3, . . .}
The set of integers Z = {. . ., −3, −2, −1, 0, 1, 2, 3, . . .}
The set of rational numbers Q = { p/q | p is an integer, q is an integer, q �= 0}
The set of prime numbers P = {2, 3, 5, 7, 11, . . .}
The set of complex numbers C = { x + i y | i
2 = −1, x, y are real numbers}
The set of real numbers R = {All decimal numbers}
The set of 2-tuples R2 = { (x, y) | x, y are real numbers }
The set of 3-tuples R3 = { (x, y, z) | x, y, z are real numbers }
The set of n-tuples Rn = { (ξ1, ξ2, . . ., ξn) | ξ1, ξ2, . . ., ξn are real numbers }
where it is understood that i is an imaginary unit with the property i2 = −1 and
decimal numbers represent all terminating and nonterminating decimals.3
(Page 3) Example 1-1. Intervals
When dealing with real numbers a, b, x it is customary to use the following notations to represent various intervals of real numbers.

Set Notation {Set} Definition Name
[a, b] {x | a ≤ x ≤ b} closed interval
(a, b) {x | a < x < b} open interval
[a, b) {x | a ≤ x < b} left-closed, right-open
(a, b] {x | a < x ≤ b} left-open, right-closed
(a,∞) {x | x > a} left-open, unbounded
[a,∞) {x | x ≥ a} left-closed,unbounded
(−∞, a) {x | x < a} unbounded, right-open
(−∞, a] {x | x ≤ a} unbounded, right-closed
(−∞,∞) R = {x | −∞ < x < ∞} Set of real numbers
Subsets
If for every element x ∈ A one can show that x is also an element of a set B,
then the set A is called a subset of B or one can say the set A is contained in the
set B. This is expressed using the mathematical statement A ⊂ B, which is read “A
is a subset of B ”. This can also be expressed by saying that B contains A, which is
written as B ⊃ A. If one can find one element of A which is not in the set B, then A
is not a subset of B. This is expressed using either of the notations A ⊂� B or B ⊃� A.
Note that the above definition implies that every set is a subset of itself, since the
elements of a set A belong to the set A. Whenever A ⊂ B and A �= B, then A is called
a proper subset of B.
Set Operations
Given two sets A and B, the union of these sets is written A ∪ B and defined
A ∪ B = { x | x ∈ A or x ∈ B, or x ∈ both A and B}
The intersection of two sets A and B is written A ∩ B and defined
A ∩ B = { x | x ∈ both A and B }
If A ∩ B is the empty set one writes A ∩ B = ∅ and then the sets A and B are said to
be disjoint.
The difference1 between two sets A and B is written A − B and defined
A − B = { x | x ∈ A and x /∈ B }
The equality of two sets is written A = B and defined A = B if and only if A ⊂ B and B ⊂ A
That is, if A ⊂ B and B ⊂ A, then the sets A and B must have the same elements
- which implies equality.
Conversely, if two sets are equal A = B, then A ⊂ B and B ⊂ A since every set is a subset of itself.
SEE FIGURE ...
 < https://www.slideshare.net/VICTORPRINCEDATEME/calculus-volume-1
< https://www.slideshare.net/VICTORPRINCEDATEME/calculus-volume-1
Figure 1-1. Selected Venn diagrams. https://en.wikipedia.org/wiki/Venn_diagram
The complement of set A - with respect to the universal set U - is written Ac and defined
Ac = { x | x ∈ U but x /∈ A }
Observe that the complement of a set A satisfies the complement laws:
A ∪ Ac = U, A ∩ Ac = ∅, ∅c = U, Uc = ∅
The operations of union ∪ and intersection ∩ satisfy the distributive laws A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
1
The difference between two sets A and B in some texts is expressed using the notation A \ B.5 and the identity laws A ∪ ∅ = A, A ∪ U = U, A ∩ U = A, A ∩ ∅ = ∅
(Page 5)
The above set operations can be illustrated using circles and rectangles, where the universal set is denoted by the rectangle and individual sets are denoted by circles.
This pictorial representation for the various set operations was devised by John Venn2 and are known as Venn diagrams. https://en.wikipedia.org/wiki/Venn_diagram
Selected Venn diagrams are illustrated in the figure 1-1.
Example 1-2. Equivalent Statements
Prove that the following statements are equivalent A ⊂ B and A ∩ B = A
[ also: https://www.mathsisfun.com/equivalent_fractions.html ]
Solution To show these statements are "equivalent" one must show:
(i) if A ⊂ B, then A ∩ B = A
and (ii) if A ∩ B = A, then it follows that A ⊂ B.
(i) Assume A ⊂ B, then if x ∈ A it follows that x ∈ B since A is a subset of B.
Consequently, one can state that x ∈ (A ∩ B), all of which implies A ⊂ (A ∩ B).
Conversely, if x ∈ (A ∩ B), then x belongs to both A and B and certainly one can
say that x ∈ A.
This implies (A ∩ B) ⊂ A. If A ⊂ (A ∩ B) and (A ∩ B) ⊂ A, then it follows that (A ∩ B) = A.
(ii) Assume A ∩ B = A, then if x ∈ A, it must also be in A ∩ B so that one can say x ∈ A and x ∈ B, which implies A ⊂ B.
Coordinate Systems
There are many different kinds of coordinate systems - most of which are created
to transform a problem or object into a simpler representation. The rectangular
coordinate system3 with axes labeled x and y provides a way of plotting number
pairs (x, y) which are interpreted as points within a plane.
2 John Venn (1834-1923) An English mathematician who studied logic and set theory.
3 Also called a cartesian coordinate system and named for Ren´e Descartes (1596-1650) a French philosopher who applied algebra to geometry problems.
( Page 6 )

Figure 1-2. Rectangular and polar coordinate systems
< https://www.slideshare.net/VICTORPRINCEDATEME/calculus-volume-1
A cartesian or rectangular coordinate system is constructed by selecting two straight lines intersecting at right angles and labeling the point of intersection as the origin of the coordinate system and then labeling the horizontal line as the x-axis and the vertical line as the y-axis.
On these axes some kind of a scale is constructed with positive numbers to the right on the horizontal axis and upward on the vertical axes. For example, by constructing lines at equally spaced distances
along the axes one can create a grid of intersecting lines.
A point in the plane defined by the two axes can then be represented by a number pair (x, y).
In rectangular coordinates a number pair (x, y) is said to have the abscissa x and the ordinate y.
The point (x, y) is located a distance r = x2 + y2 from the origin with x representing distance of the point from the y-axis and y representing the distance of the point from the x-axis.
The x axis or abscissa axis and the y axis or ordinate axis divides the plane into four quadrants
(counter-clockwise) labeled I, II, III and IV .

 hhhh
hhhh 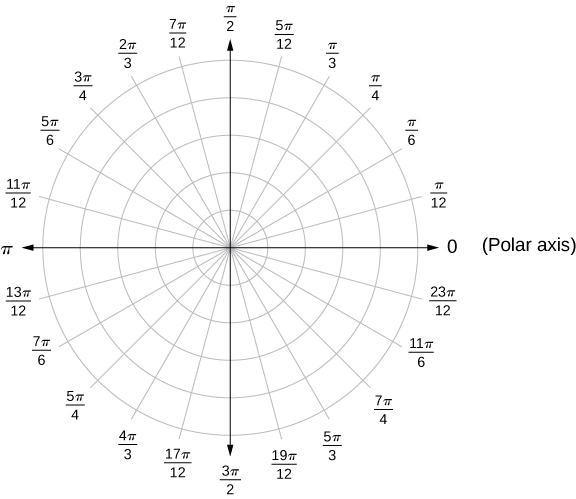
To construct a polar coordinate system - one selects an origin for the polar coordinates and labels it 0.
Next, construct a half-line similar to the x-axis of the rectangular coordinates. This half-line is called the polar axis or initial ray and the origin is called the pole of the polar coordinate system.
By placing another line on top of the polar axis and rotating this line about the pole through a positive angle θ, measured in radians, one can create a ray emanating from the origin at an angle θ
as illustrated in the figure 1-3.
In polar coordinates the rays are illustrated emanating from the origin at equally spaced angular distances around the origin and then concentric circles are constructed representing constant distances from the origin.
Page 7
A point in polar coordinates is then denoted by the number pair (r, θ) where θ is the angle of rotation associated with the ray and r is a distance outward from the origin along the ray.
The polar origin or pole has the coordinates (0, θ) for any angle θ.
All points having the polar coordinates (ρ, 0), with ρ ≥ 0, lie on the polar axis.
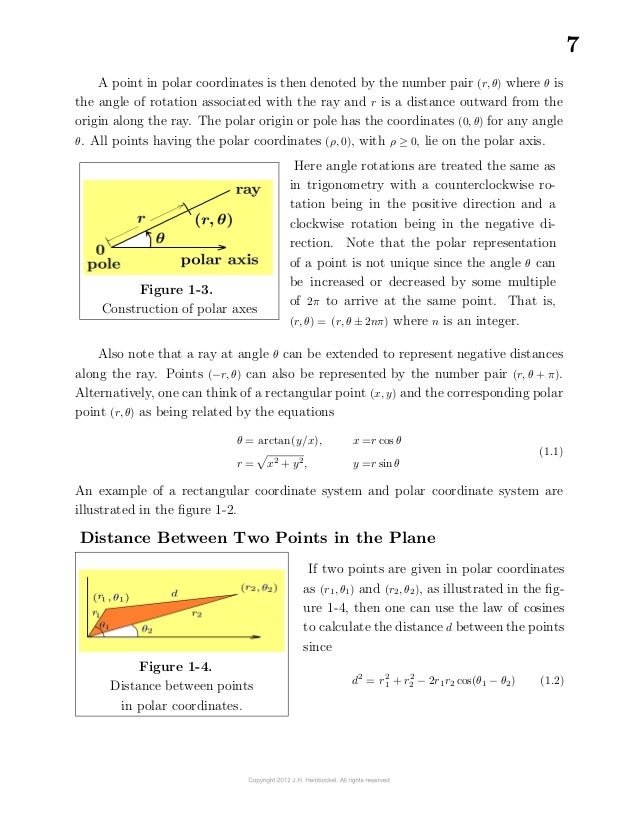
Figure 1-3. Construction of polar axes < https://www.slideshare.net/VICTORPRINCEDATEME/calculus-volume-1
Here angle rotations are treated the same as in trigonometry with a counterclockwise rotation being in the positive direction and a clockwise rotation being in the negative direction.
Note that the polar representation of a point is not unique since the angle θ can be increased or decreased by some multipleof 2π to arrive at the same point.
That is, (r, θ) = (r, θ ± 2nπ) where n is an integer.
Also note that a ray at angle θ can be extended to represent negative distances along the ray. Points (−r, θ) can also be represented by the number pair (r, θ + π).
Alternatively, one can think of a rectangular point (x, y) and the corresponding polar
point (r, θ) as being related by the equations :
equation (1.1)
θ = arctan (y/x), x =r cos θ
r = x2 + y2+ y2, y=r sin θ
An example of a rectangular coordinate system and polar coordinate system are illustrated in the figure 1-2.
Distance Between Two Points in the Plane
Figure 1-4. Distance between points in polar coordinates. (above)
If two points are given in polar coordinates as (r1, θ1) and (r2, θ2), as illustrated in the figure 1-4, then one can use the law of cosines [trigonometry] to calculate the distance d between the points since
equation (1.2)
d2 = r2 1 + r2 2 2r1r2 cos(θ1 − θ2)
Page 8
Alternatively, let (x1, y1) and (x2, y2) denote two points which are plotted on a
cartesian set of axes as illustrated in the figure 1-5. The Greek letter ∆ (delta) is
used to denote a change in a quantity. For example, in moving from the point (x1, y1)
to the point (x2, y2) the change in x is denoted ∆x = x2 − x1 and the change in y is
denoted ∆y = y2 − y1. These changes can be thought of as the legs of a right-triangle
as illustrated in the figure 1-5.
Figure 1-5. Using a right-triangle to calculate distance between two points in rectangular coordinates.
< https://www.slideshare.net/VICTORPRINCEDATEME/calculus-volume-1
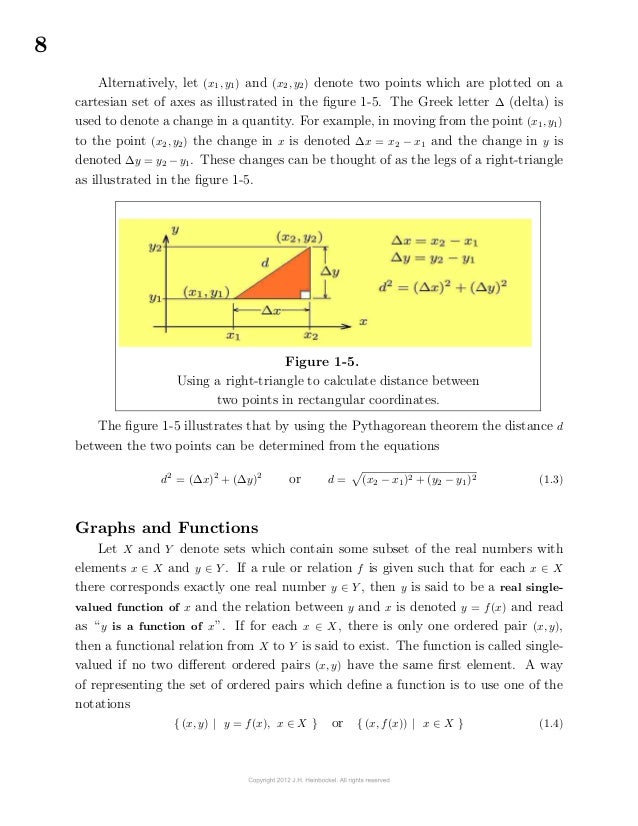
The figure 1-5 illustrates that by using the Pythagorean theorem the distance d between the two points can be determined from the equations
d2 = (∆x)
2 + (∆y)
2 or d = �(x2 − x1)2 + (y2 − y1)2 (1.3)
Graphs and Functions
Let X and Y denote sets which contain some subset of the real numbers with elements x ∈ X and y ∈ Y .
If a rule or relation f is given such that for each x ∈ X there corresponds exactly one real number y ∈ Y , then y is said to be a real single valued function of x and the relation between y and x is denoted y = f(x) and read
as “y is a function of x”. If for each x ∈ X, there is only one ordered pair (x, y),
then a functional relation from X to Y is said to exist. The function is called single�valued if no two different ordered pairs (x, y) have the same first element. A way of representing the set of ordered pairs which define a function is to use one of the
notations
{ (x, y) | y = f(x), x ∈ X } or { (x, f(x)) | x ∈ X } (1.4)9
The set of values x ∈ X is called the domain of definition of the function f(x).
The set of values {y | y = f(x), x ∈ X} is called the range of the function or the image of the set X under the mapping or transformation given by f. The set of ordered pairs
C = { (x, y) | y = f(x), x ∈ X}
is called the graph of the function and represents a curve in the x, y-plane giving
a pictorial representation of the function. If y = f(x) for x ∈ X, the number x is
called the independent variable or argument of the function and the image value
y is called the dependent variable of the function. It is to be understood that the
domain of definition of a function contains real values for x for which the relation
f(x) is also real-valued. In many physical problems, the domain of definition X must
be restricted in order that a given physical problem be well defined. For example,
in order that √x − 1 be real-valued, x must be restricted to be greater than or equal
to 1.
When representing many different functions the symbol f can be replaced by
any of the letters from the alphabet. For example, one might have several different
functions labeled as
y = f(x), y = g(x), y = h(x), . . ., y = y(x), . . ., y = z(x) (1.5)
or one could add subscripts to the letter f to denote a set of n-different functions
F = {f1(x), f2(x), . . ., fn(x)} (1.6)
Example 1-3. (Functions)
(a) Functions defined by a formula over a given domain.
Let y = f(x) = x2 + x for x ∈ R be a given rule defining a function which can
be represented by a curve in the cartesian x, y-plane. The variable x is a dummy
variable used to define the function rule. Substituting the value 3 in place of x in
the function rule gives y = f(3) = 32 + 3 = 12 which represents the height of the curve
at x = 3. In general, for any given value of x the quantity y = f(x) represents the
height of the curve at the point x. By assigning a collection of ordered values to x
and calculating the corresponding value y = f(x), using the given rule, one collects
a set of (x, y) pairs which can be interpreted as representing a set of points in the
cartesian coordinate system. The set of all points corresponding to a given rule is10
called the locus of points satisfying the rule.
The graph illustrated in the figure 1-6 is a pictorial representation of the given rule.
x y = f(x) = x2 + x
-2.0 2.00
-1.8 1.44
-1.6 0.96
-1.4 0.56
-1.2 0.24
-1.0 0.00
-0.8 -0.16
-0.6 -0.24
-0.4 -0.24
-0.2 -0.16
0.0 0.00
0.2 0.24
0.4 0.56
0.6 0.96
0.8 1.44
1.0 2.00
1.2 2.64
1.4 3.36
1.6 4.16
1.8 5.04
2.0 6.00

Figure 1-6. A graph of the function y = f(x) = x2 + x
Note that substituting x + h in place of x in the function rule gives
f(x + h) = (x + h)
2 + (x + h) = x2 + (2h + 1)x + (h2 + h).
If f(x) represents the height of the curve at the point x, then f(x + h) represents the
height of the curve at x + h.
(b) Let r = f(θ) = 1 + θ for 0 ≤ θ ≤ 2π be a given rule defining a function which
can be represented by a curve in polar coordinates (r, θ). One can select a set
of ordered values for θ in the interval [0, 2π] and calculate the corresponding
values for r = f(θ). The set of points (r, θ) created can then be plotted on polar
graph paper to give a pictorial representation of the function rule. The graph
illustrated in the figure 1-7 is a pictorial representation of the given function
over the given domain.
Note in dealing with polar coordinates a radial distance r and polar angle θ can
have any of the representations
( (−1)nr, θ + nπ)11
and consequently a functional relation like r = f(θ) can be represented by one of the
alternative equations r = (−1)nf(θ + nπ)
θ r = f(θ) = 1 + θ
0 1 + 0
π/4 1 + π/4
2π/4 1 + 2π/4
3π/4 1 + 3π/4
4π/4 1 + 4π/4
5π/4 1 + 5π/4
6π/4 1 + 6π/4
7π/4 1 + 7π/4
8π/4 1 + 8π/4
 hhhh
hhhh 

Figure 1-7. A polar plot of the function r = f(θ) = 1 + θ
(c)
The absolute value function
The absolute value function is defined
y = f(x) =| x |=
� x, x ≥ 0
−x, x ≤ 0
Substituting in a couple of specific values for x one can
form a set of (x, y) number pairs and then sketch a graph
of the function, which represents a pictorial image of the functional relationship
between x and y.
(d) Functions defined in a piecewise fashion.
A function defined by
f(x) =
1 + x, x ≤ −1
1 − x, −1 ≤ x ≤ 0
x2, 0 ≤ x ≤ 2
2 + x, x > 2
x ∈ R
is a collection of rules which defines the function in a piecewise fashion. One must
examine values of the input x to determine which portion of the rule is to be used
in evaluating the function. The above example illustrates a function having jump
discontinuities at the points where x = −1 and x = 0.
Page 12
(e) Numerical data.
If one collects numerical data from an experiment such as recording temperature
T at different times t, then one obtains a set of data points called number pairs. If
these number pairs are labeled (ti, Ti), for i = 1, 2, . . ., n, one obtains a table of values
such as
Time t t1 t2 · · · tn
Temperature T T1 T2 · · · Tn
It is then possible to plot a t, T-axes graph associated with these data points by plot�ting the points and then drawing a smooth curve through the points or by connecting
the points with straight line segments. In doing this, one is assuming that the curve
sketched is a graphical representation of an unknown functional relationship between
the variables.
(f) Other representation of functions
Functions can be represented by different methods such as using equations,
graphs, tables of values, a verbal rule, or by using a machine like a pocket cal�culator which is programmable to give some output for a given input. Functions can
be continuous or they can have discontinuities. Continuous functions are recognized
by their graphs which are smooth unbroken curves with continuously turning tangent
lines at each point on the curve. Discontinuities usually occur when functional values
or tangent lines are not well defined at a point.
Increasing and Decreasing Functions
One aspect in the study of calculus is to examine how functions change over an
interval. A function is said to be increasing over an interval (a, b) if for every pair
of points (x0, x1) within the interval (a, b), satisfying x0 < x1, the height of the curve
at x0 is less than the height of the curve at x1 or f(x0) < f(x1). A function is called
decreasing over an interval (a, b) if for every pair of points (x0, x1) within the interval
(a, b), satisfying x0 < x1, one finds the height of the curve at x0 is greater than the
height of the curve at x1 or f(x0) > f(x1).
Page 13
Linear Dependence and Independence
A linear combination of a set of functions {f1, f2, . . ., fn} is formed by taking
arbitrary constants c1, c2, . . ., cn and forming the sum
y = c1f1 + c2f2 + · · · + cnfn (1.7)
One can then say that y is a linear combination of the set of functions {f1, f2, . . ., fn}.
If a function f1(x) is some constant c times another function f2(x), then one can
write f1(x) = cf2(x) and under this condition the function f1 is said to be linearly
dependent upon f2. If no such constant c exists, then the functions are said to
be linearly independent. Another way of expressing linear dependence and linear
independence applied to functions f1 and f2 is as follows. One can say that, if there
are nonzero constants c1, c2 such that the linear combination
c1f1(x) + c2f2(x) = 0 (1.8)
for all values of x, then the set of functions {f1, f2} is called a set of dependent
functions. This is due to the fact that if c1 �= 0, then one can divided by c1 and
express the equation (1.8) in the form f1(x) = −c2
c1 f2(x) = cf2(x). If the only constants
which make equation (1.8) a true statement are c1 = 0 and c2 = 0, then the set of
functions {f1, f2} is called a set of linearly independent functions.
An immediate generalization of the above is the following. If there exists con�stants c1, c2, . . ., cn, not all zero, such that the linear combination
c1f1(x) + c2f2(x) + · · · cnfn(x) = 0, (1.9)
for all values of x, then the set of functions {f1, f2, . . ., fn} is called a linearly dependent
set of functions. If the only constants, for which equation (1.9) is true, are when
c1 = c2 = · · · = cn = 0, then the set of functions {f1, f2, . . ., fn} is called a linearly
independent set of functions. Note that if the set of functions are linearly dependent,
then one of the functions can be made to become a linear combination of the other
functions. For example, assume that c1 �= 0 in equation (1.9). One can then write
f1(x) = −c2
c1
f2(x) − · · · − cn
c1
fn(x)
which shows that f1 is some linear combination of the other functions. That is, f1
is dependent upon the values of the other functions.
Page 14
Single-valued Functions
Consider plane curves represented in rectangular coordinates such as the curves
illustrated in the figures 1-8. These curves can be considered as a set of ordered
pairs (x, y) where the x and y values satisfy some specified condition.

Figure 1-8. Selected curves sketched in rectangular coordinates
In terms of a set representation, these curves can be described using the set
notation
C = { (x, y) | relationship satisfied by x and y with x ∈ X }
This represents a collection of points (x, y), where x is restricted to values from some
set X and y is related to x in some fashion. A graph of the function results when the
points of the set are plotted in rectangular coordinates. If for all values x0 a vertical
line x = x0 cuts the graph of the function in only a single point, then the function is
called single-valued. If the vertical line intersects the graph of the function in more
than one point, then the function is called multiple-valued.
Similarly, in polar coordinates, a graph of the function is a curve which can be
represented by a collection of ordered pairs (r, θ). For example,
C = { (r, θ) | relationship satisfied by r and θ with θ ∈ Θ }
where Θ is some specified domain of definition of the function. There are available
many plotting programs for the computer which produce a variety of specialized
graphs. Some computer programs produce not only cartesian plots and polar plots,
but also many other specialized graph types needed for various science and engineer�ing applications. These other graph types give an alternative way of representing
functional relationships between variables.15
Example 1-4. Rectangular and Polar Graphs
Plotting the same function in both rectangular coordinates and polar coordinates
gives different shaped curves and so the graphs of these functions have different
properties depending upon the coordinate system used to represent the function.
For example, plot the function y = f(x) = x2 for −2 ≤ x ≤ 2 in rectangular coordinates
and then plot the function r = g(θ) = θ2 for 0 ≤ θ ≤ 2π in polar coordinates. Show
that one curve is a parabola and the other curve is a spiral.
Solution
x y = f(x) = x2
-2.00 4.0000
-1.75 3.0625
-1.50 2.2500
-1.25 1.5625
-1.00 1.0000
-0.75 0.5625
-0.50 0.2500
-0.25 0.0625
0.00 0.0000
0.25 0.0625
0.50 0.2500
0.75 0.5625
1.00 1.0000
1.25 1.5625
1.50 2.2500
1.75 3.0625
2.00 4.0000
θ r = g(θ) = θ2
0.00 0.0000
π/4 π2/16
π/2 π2/4
3π/4 9π2/16
π π2
5π/4 25π2/16
3π/2 9π2/4
7π/4 49π2/16
2π 4π2
C1 = { (x, y) | y = f(x) = x2, −2 ≤ x ≤ 2 } C2 = { (r, θ) | r = g(θ) = θ2, 0 ≤ θ ≤ 2π }

Figure 1-9. Rectangular and polar graphs give different pictures of function.
Select some points x from the domain of the function and calculate the image
points under the mapping y = f(x) = x2. For example, one can use a spread sheet
and put values of x in one column and the image values y in an adjacent column
to obtain a table of values for representing the function at a discrete set of selected
points.
Page 16
Similarly, select some points θ from the domain of the function to be plotted in
polar coordinates and calculate the image points under the mapping r = g(θ) = θ2.
Use a spread sheet and put values of θ in one column and the image values r in an
adjacent column to obtain a table for representing the function as a discrete set of
selected points. Using an x spacing of 0.25 between points for the rectangular graph
and a θ spacing of π/4 for the polar graph, one can verify the table of values and
graphs given in the figure 1-9.
Some well known cartesian curves are illustrated in the following figures.

Figure 1-10. Polynomial curves y = x, y = x2 and y = x3
Figure 1-11. The trigonometric functions y = sin x and y = cos x for −π ≤ x ≤ 2π.17
Some well known polar curves are illustrated in the following figures.
b= -a, b=2a, b=3a

Figure 1-12. The limac¸on curves r = 2a cos θ + b
r = a sin 3θ r = a cos 2θ r = a sin 5θ
Figure 1-13. The rose curves r = a cos nθ and r = a sin nθ
If n odd, curve has n-loops and if n is even, curve has 2n loops.
Parametric Representation of Curve
Examine the graph in figure 1-8(b) and observe that it does not represent a
single-valued function y = f(x). Also the circle in figure 1-8(c) does not define a
single valued function. An alternative way of graphing a function is to represent
it in a parametric form.4 In general, a graphical representation of a function or a
4 The parametric form for representing a curve is not unique and the parameter used may or may not have a
physical meaning.18
section of a function, be it single-valued or multiple-valued, can be defined by a
parametric representation
C = {(x, y) | x = x(t), y = y(t), a ≤ t ≤ b} (1.10)
where both x(t) and y(t) are single-valued functions of the parameter t. The re�lationship between x and y is obtained by eliminating the parameter t from the
representation x = x(t) and y = y(t). For example, the parametric representation
x = x(t) = t and y = y(t) = t
2, for t ∈ R, is one parametric representation of the
parabola y = x2.
The Equation of a Circle
A circle of radius ρ and centered at
the point (h, k) is illustrated in the figure
1-14 and is defined as the set of all points
(x, y) whose distance from the point (h, k)
has the constant value of ρ. Using the dis�tance formula (1.3), with (x1, y1) replaced
by (h, k), the point (x2, y2) replaced by the
variable point (x, y) and replacing d by ρ,
one can show the equation of the circle is
given by one of the formulas
Equation (1.11)
(x − h)2 + (y − k)2 = ρ2 / [square root] (x − h)2 + (y − k)2 = ρ
or

Figure 1-14. Circle centered at (h, k).
Equations of the form:
Equation (1.12)
x2 + y2 + αx + βy + γ = 0, α, β, γ constants
can be converted to the form of equation (1.11) by completing the square on the
x and y terms.
This is accomplished by taking 1/2 of the x-coefficient, squaring
and adding the result to both sides of equation (1.12) and then taking 1/2 of the
y-coefficient, squaring and adding the result to both sides of equation (1.12). One
then obtains
Page 19
�
x2 + αx +
α2
4
�
+
�
y2 + βy + β2
4
�
= α2
4 + β2
4 − γ
which simplifies to �
x +
α
2
�2
+
�
y + β
2
�2
= r2
where r2 = α2
4 + β2
4 − γ. Completing the square is a valid conversion whenever the
right-hand side α2
4 + β2
4 − γ ≥ 0.
An alternative method of representing the equation of the circle is to introduce
a parameter θ such as the angle illustrated in the figure 1-14 and observe that by
trigonometry
sin θ = y − k
ρ
and cos θ = x − h
ρ
These equations are used to represent the circle in the alternative form
C = { (x, y) | x = h + ρ cos θ, y = k + ρ sin θ, 0 ≤ θ ≤ 2π } (1.13)
This is called a parametric representation of the circle in terms of a parameter θ.

Figure 1-15. Circle centered at (r1, θ1).
The equation of a circle in polar form can
be constructed as follows. Let (r, θ) denote
a variable point which moves along the circumference of a circle of radius ρ which is
centered at the point (r1, θ1) as illustrated
in the figure 1-15. Using the distances r, r1
and ρ, one can employ the law of cosines
to express the polar form of the equation
of a circle as
r2 + r2
1 − 2rr1 cos(θ − θ1) = ρ2 (1.14)
Functions can be represented in a variety of ways. Sometimes functions are
represented in the implicit form G(x, y) = 0, because it is not always possible to
solve for one variable explicitly in terms of another. In those cases where it is
possible to solve for one variable in terms of another to obtain y = f(x) or x = g(y),
the function is said to be represented in an explicit form.20
For example, the circle of radius ρ can be represented by any of the relations
G(x, y) =x2 + y2 − ρ2 = 0,
y = f(x) = � +
�ρ2 − x2, −ρ ≤ x ≤ ρ
−
�ρ2 − x2, −ρ ≤ x ≤ ρ
, x = g(y) = � +
�ρ2 − y2, −ρ ≤ y ≤ ρ
−
�ρ2 − y2, −ρ ≤ y ≤ ρ
(1.15)
Note that the circle in figure 1-8(c) does not define a single valued function. The
circle can be thought of as a graph of two single-valued functions y = +�ρ2 − x2
and y = −
�ρ2 − x2 for −ρ ≤ x ≤ ρ if one treats y as a function of x. The other
representation in equation (1.15) results if one treats x as a function of y.
Types of functions
One can define a functional relationships between the two variables x and y in different ways.
A polynomial function in the variable x has the form
y = pn(x) = a0xn + a1xn−1 + a2xn−2 + · · · + an−1x + an (1.16)
where a0, a1, . . ., an represent constants with a0 �= 0 and n is a positive integer.
The integer n is called the degree of the polynomial function.
The fundamental theorem of algebra states that a polynomial of degree n has n-roots.
That is, the polynomial equation pn(x) = 0 has n-solutions called the roots of the polynomial equation. If
these roots are denoted by x1, x2, . . ., xn, then the polynomial can also be represented in the form
pn(x) = a0(x − x1)(x − x2)· · ·(x − xn)
If xi is a number, real or complex, which satisfies pn(xi) = 0, then (x−xi) is a factor of the polynomial function pn(x).
Complex roots of a polynomial function must always
occur in conjugate pairs and one can say that if α + i β is a root of pn(x) = 0, then
α− i β is also a root. Real roots xi of a polynomial function give rise to linear factors
(x − xi), while complex roots of a polynomial function give rise to quadratic factors
of the form �
(x − α)2 + β2�
, α, β constant terms.
A rational function is any function of the form
y = f(x) = P(x)
Q(x) (1.17)
where both P(x) and Q(x) are polynomial functions in x and Q(x) �= 0. If y = f(x) is
a root of an equation of the form
b0(x)yn + b1(x)yn−1 + b2(x)yn−2 + · · · + bn−1(x)y + bn(x) = 0 (1.18)21
where b0(x), b1(x), . . ., bn(x) are polynomial functions of x and n is a positive integer,
then y = f(x) is called an algebraic function. Note that polynomial functions and
rational functions are special types of algebraic functions.
Functions which are built
up from a finite number of operations of the five basic operations of addition, sub�traction, multiplication, division and extraction of integer roots, usually represent algebraic functions.
Some examples of algebraic functions are
1. Any polynomial function.
2. f1(x) = (x3 + 1)√x + 4
3. f2(x) = x2 + √3 6 + x2 (x − 3)4/3
The function f(x) = √
x2 is an example of a function which is not an algebraic func�tion.
This is because the square root of x2 is the absolute value of x and represented
f(x) = √
x2 = |x| =
� x, if x ≥ 0
−x, if x < 0
and the absolute value operation is not one of the five basic operations mentioned above.
A transcendental function is any function which is not an algebraic function.
The exponential functions, logarithmic functions, trigonometric functions, inverse
trigonometric functions, hyperbolic functions and inverse hyperbolic functions are
examples of transcendental functions considered in this calculus text.
The Exponential and Logarithmic Functions
The exponential functions have the form y = bx, where b > 0 is a positive constant
and the variable x is an exponent. If x = n is a positive integer, one defines
bn = b · b · · · b
��
n factors
and b−n = 1
bn (1.19)
By definition, if x = 0, then b0 = 1. Note that if y = bx, then y > 0 for all real values
of x.
[ https://www.reed.edu/academic_support/pdfs/qskills/logarithms.pdf ] < definition
Logarithmic functions and exponential functions are related.
By definition,
if y = bx then x = logb y (1.20) and x, the exponent, is called the "logarithm of y to the base b".
Consequently, one
can write
logb(bx) = x for every x ∈ R and blogb x = x for every x > 0 (1.21)22
Recall that logarithms satisfy the following properties
logb(xy) = logb x + logb y, x > 0 and y > 0
logb
�x
y
�
= logb x − logb y, x > 0 and y > 0
logb(yx) = x logb y, x can be any real number
(1.22)
Of all the numbers b > 0 available for use as a base for the logarithm function
the base b = 10 and base b = e = 2.71818 · · · are the most often seen in engineering
and scientific research.
The number e is a physical constant 5 like π.
It can not be represented as the ratio of two integer so is an irrational number. It can be defined
as the limiting sum of the infinite series
e = 1
0! +
1
1! +
1
2! +
1
3! +
1
4! +
1
5! + · · · +
1
n!
+ · · ·
Using a computer one can verify that the numerical value of e to 50 decimal places
is given by
e = 2.7182818284590452353602874713526624977572470936999 . . .
The irrational number e can also be determined from the limit e = lim
h→0 (1 + h)
1/h.
In the early part of the seventeenth century many mathematicians dealt with
and calculated the number e, but it was Leibnitz in 1690 who first gave it a name
and notation.
His notation for the representation of e didn’t catch on.
The value of the number represented by the limit lim
h→0
(1 + h)
1/h is used so much in mathematics
it was represented using the symbol e by Leonhard Euler sometime around 1731
and his notation for representing this number has been used ever since.
The number e is sometimes referred to as Euler’s number, the base of the natural logarithms.
[ https://en.wikipedia.org/wiki/E_(mathematical_constant) ]
The number e and the exponential function ex will occur frequently in our study of calculus.
5 There are many physical constants in mathematics.
Some examples are e, π, i,(imaginary component), γ (Euler-Mascheroni constant).
For a listing of additional mathematical constants go to the web site
http : //en.wikipedia.org/wiki/Mathematical constant. ( https://en.wikipedia.org/wiki/Mathematical_constant )
6 One can go to the web site:
http://www.numberworld.org/misc_runs/e-500b.html to see that over 500 billion digits of this number havebeen calculated.
7 Gottfried Wilhelm Leibnitz (1646-1716) a German physicist, mathematician.
8 Leonhard Euler (1707-1783) a famous Swiss mathematician.
Page 23
The logarithm to the base e, is called the natural logarithm and its properties are developed in a later chapter.
The natural logarithm is given a special notation.
Whenever the base b = e one can write either
y = loge x = ln x or y = log x (1.23)
That is, if the notation ln is used or whenever the base is not specified in using
logarithms, it is to be understood that the base b = e is being employed. In this
special case one can show
y = ex = exp(x) ⇐⇒ x = ln y (1.24)
which gives the identities
ln(ex) = x, x ∈ R and eln x = x, x > 0 (1.25)
In our study of calculus it will be demonstrated that the natural logarithm has the
special value ln(e) = 1.

Figure 1-16. The exponential function y = ex and logarithmic function y = ln x
Note that if y = logb x, then one can write the equivalent statement by = x since a
logarithm is an exponent. Taking the natural logarithm of both sides of this last
equation gives
ln(by) = ln x or y ln b = ln x (1.26)24
Consequently, for any positive number b different from one
y = logb x = ln x
ln b
, b �= 1 (1.27)
The exponential function y = ex, together with the natural logarithm function can
then be used to define all exponential functions by employing the identity
y = bx = (eln b)x = ex ln b (1.28)
Graphs of the exponential function y = ex = exp(x) and the natural logarithmic
function y = ln(x) = log(x) are illustrated in the figure 1-16.
The Trigonometric Functions
The ratio of sides of a right triangle are used to define the six trigonometric
functions associated with one of the acute angles of a right triangle.
These definitions
can then be extended to apply to positive and negative angles associated with a point
moving on a unit circle.
The six trigonometric functions associated with a right triangle are:
sine
cosine
tangent
cotangent
secant
cosecant
which are abbreviated respectively as:
sin, tan, sec, cos, cot, and csc .
Let θ [Theta] and ψ [Psi] denote complementary angles in a right triangle as illustrated above.
The six trigonometric functions associated with the angle θ ("Theta") are:
sin θ = y
r = opposite side
hypotenuse ,
cos θ = x
r = adjacent side
hypotenuse ,
tan θ = y
x = opposite side
adjacent side,
cot θ = x
y = adjacent side
opposite side,
sec θ = r
x = hypotenuse
adjacent side
csc θ = r
y = hypotenuse
opposite side
Graphs of the Trigonometric Functions
Graphs of the trigonometric functions sin θ, cos θ and tan θ, for θ varying over the
domain 0 ≤ θ ≤ 4π, can be represented in rectangular coordinates by the point sets
S ={ (θ, y) | y = sin θ, 0 ≤ θ ≤ 4π },
C ={ (θ, x) | x = cos θ, 0 ≤ θ ≤ 4π }
T ={ (θ, y) | y = tan θ, 0 ≤ θ ≤ 4π }
and are illustrated in the figure 1-17.25
Using the periodic properties
sin(θ + 2π) = sin θ, cos(θ + 2π) = cos θ and tan(θ + π) = tan θ
these graphs can be extend and plotted over other domains.

Figure 1-17. Graphs of the trigonometric functions sin θ, cos θ and tan θ
The function y = sin θ can also be interpreted as representing the motion of a point P
moving on the circumference of a unit circle. The point P starts at the point (1, 0),
where the angle θ is zero and then moves in a counterclockwise direction about the
circle. As the point P moves around the circle its ordinate value is plotted against
the angle θ. The situation is as illustrated in the figure 1-17(a). The function x = cos θ
can be interpreted in the same way with the point P moving on a circle but starting
at a point which is shifted π/2 radians clockwise. This is the equivalent to rotating
the x, y−axes for the circle by π/2 radians and starting the point P at the coordinate
(1, 0) as illustrated in the figure 1-17(b).
The Hyperbolic Functions
Related to the exponential functions ex and e−x are the hyperbolic functions
hyperbolic sine written sinh,
hyperbolic cosine written cosh,
hyperbolic tangent written tanh,
hyperbolic cotangent written coth
hyperbolic secant written sech
hyperbolic cosecant written csch26
These functions are defined
sinhx =ex − e−x
2 ,
coshx =ex + e−x
2 ,
tanhx = sinhx
coshx,
cschx = 1
sinhx
sechx = 1
coshx
cothx = 1
tanhx
(1.29)
As the trigonometric functions are related to the circle and are sometimes referred
to as circular functions, it has been found that the hyperbolic functions are related
to equilateral hyperbola and hence the name hyperbolic functions. This will be
explained in more detail in the next chapter.
Symmetry of Functions
The expression y = f(x) is the representation of a function in an explicit form
where one variable is expressed in terms of a second variable. The set of values given
by
S = {(x, y) | y = f(x), x ∈ X}
where X is the domain of the function, represents a graph of the function.
The notation f(x), read “f of x”, has the physical interpretation of representing y which is the height of the curve at the point x.
Given a function y = f(x), one can replace x by any other argument. For example, if f(x) is a periodic function with least
period T, one can write f(x) = f(x + T) for all values of x. One can interpret the
equation f(x) = f(x + T) for all values of x as stating that the height of the curve at
any point x is the same as the height of the curve at the point x + T. As another
example, if the notation y = f(x) represents the height of the curve at the point x,
then y + ∆y = f(x + ∆x) would represent the height of the given curve at the point
x+∆x and ∆y = f(x+∆x)−f(x) would represent the change in the height of the curve
y in moving from the point x to the point x+ ∆x. If the argument x of the function
is replaced by −x, then one can compare the height of the curve at the points x and
−x. If f(x) = f(−x) for all values of x, then the height of the curve at x equals the
height of the curve at −x and when this happens the function f(x) is called an even
function of x and one can state that f(x) is a symmetric function about the y-axis.
If f(x) = −f(−x) for all values of x, then the height of the curve at x equals the
negative of the height of the curve at −x and in this case the function f(x) is called
an odd function of x and one can state that the function f(x) is symmetric about the
origin. By interchanging the roles of x and y and shifting or rotation of axes, other27
symmetries can be discovered. The figure 1-18 and 1-19 illustrates some examples
of symmetric functions.

Figure 1-18. Examples of symmetric functions
Symmetry about a line. Symmetry about a point.
Figure 1-19. Examples of symmetric functions
In general, two points P1 and P2 are said to be symmetric to a line if the line is
the perpendicular bisector of the line segment joining the two points. In a similar
fashion a graph is said to symmetric to a line if all points of the graph can be
grouped into pairs which are symmetric to the line and then the line is called the
axis of symmetry of the graph. A point of symmetry occurs if all points on the graph
can be grouped into pairs so that all the line segments joining the pairs are then
bisected by the same point. See for example the figure 1-19. For example, one can
say that a curve is symmetric with respect to the x-axis if for each point (x, y) on the
curve, the point (x, −y) is also on the curve. A curve is symmetric with respect to
the y-axis if for each point (x, y) on the curve, the point (−x, y) is also on the curve.
A curve is said to be symmetric about the origin if for each point (x, y) on the curve,
then the point (−x, −y) is also on the curve.28
Example 1-5. A polynomial function pn(x) = a0xn + a1xn−1 + · · · + an−1x + an of
degree n has the following properties.
(i) If only even powers of x occur in pn(x), then the polynomial curve is symmetric
about the y-axis, because in this case pn(−x) = pn(x).
(ii) If only odd powers of x occur in pn(x), then the polynomial curve is symmetric
about the origin, because in this case pn(−x) = −pn(x).
(iii) If there are points x = a and x = c such that pn(a) and pn(c) have opposite signs,
then there exists at least one point x = b satisfying a < b < c, such that pn(b) = 0.
This is because polynomial functions are continuous functions and they must
change continuously from the value pn(a) to the value pn(c) and so must pass, at
least once, through the value zero.
Translation and Scaling of Axes
Consider two sets of axes labeled (x, y) and (¯x, y¯) as illustrated in the figure 1-
20(a) and (b).
Pick up the (¯x, y¯) axes and keep the axes parallel to each other and
place the barred axes at some point P having the coordinates (h, k) on the (x, y) axes
as illustrated in the figure 1-20(c).
One can now think of the barred axes as being
a translated set of axes where the new origin has been translated to the point (h, k)
of the old set of unbarred axes. How is an arbitrary point (x, y) represented in terms
of the new barred axes coordinates? An examination of the figure 1-20 shows that
a general point (x, y) can be represented as
x = ¯x + h and y = ¯y + k or x¯ = x − h and y¯ = y − k (1.30)
Consider a curve y = f(x) sketched on the (x, y) axes of figure 1-20(a). Change
the symbols x and y to x¯ and y¯ and sketch the curve y¯ = f(¯x) on the (¯x, y¯) axes of
figure 1-20(b). The two curves should look exactly the same, the only difference
being how the curves are labeled. Now move the (¯x, y¯) axes to a point (h, k) of the
(x, y) coordinate system to produce a situation where the curve y¯ = f(¯x) is now to be
represented with respect to the (x, y) coordinate system.
The new representation can be determined by using the transformation equations
(1.30). That is, the new representation of the curve is obtained by replacing y¯ by
y − k and replacing x¯ by x − h to obtain
y − k = f(x − h) (1.31) 29

Figure 1-20. Shifting of axes.
In the special case k = 0, the curve y = f(x − h) represents a shifting of the curve
y = f(x) a distance of h units to the right. Replacing h by −h and letting k = 0 one
finds the curve y = f(x + h) is a shifting of the curve y = f(x) a distance of h units
to the left. In the special case h = 0 and k �= 0, the curve y = f(x) + k represents a
shifting of the graph y = f(x) a distance of k units upwards. In a similar fashion,
the curve y = f(x) − k represents a shifting of the graph of y = f(x) a distance of k
units downward. The figure 1-21 illustrates the shifting and translation of axes for
the function y = f(x) = x2.
Figure 1-21. Translation and shifting of axes.
Introducing a constant scaling factor s > 0, by replacing y by y/s one can create
the scaled function y = sf(x). Alternatively one can replace x by sx and obtain the
scaled function y = f(sx). These functions are interpreted as follows.
(1) Plotting the function y = sf(x) has the effect of expanding the graph of y = f(x)
in the vertical direction if s > 1 and compresses the graph if s < 1. This is30
equivalent to changing the scaling of the units on the y-axis in plotting a graph.
As an exercise plot graphs of y = sin x, y = 5 sin x and y = 1
5 sin x.
(2) Plotting the function y = f(sx) has the effect of expanding the graph of y = f(x)
in the horizontal direction if s < 1 and compresses the graph in the x-direction
if s > 1. This is equivalent to changing the scaling of the units on the x-axis in
plotting a graph. As an exercise plot graphs of y = sin x, y = sin( 1
3x) and y = sin(3x).
(3) A plot of the graph (x, −f(x)) gives a reflection of the graph y = f(x) with respect
to the x-axis.
(4) A plot of the graph (x, f(−x)) gives a reflection of the graph y = f(x) with respect
to the y-axis.
Rotation of Axes
Place the (¯x, y¯) axes from figure 1-20(b) on top of the (x, y) axes of figure 1-20(a)
and then rotate the (¯x, y¯) axes through an angle θ to obtain the figure 1-22. An
arbitrary point (x, y), a distance r from the origin, has the coordinates (¯x, y¯) when
referenced to the (¯x, y¯) coordinate system. Using basic trigonometry one can find
the relationship between the rotated and unrotated axes. Examine the figure 1-22
and verify the following trigonometric relationships.
The projection of r onto the x¯ axis produces x¯ = r cos φ and the projection of r onto
the y¯ axis produces y¯ = r sin φ. In a similar fashion consider the projection of r onto
the y-axis to show y = r sin(θ + φ) and the projection of r onto the x-axis produces
x = r cos(θ + φ).31

Figure 1-22. Rotation of axes.
Expressing these projections in the form
cos(θ + φ) = x
r
sin(θ + φ) = y
r
(1.32)
cos φ = x¯
r
sinφ = y¯
r
(1.33)
one can expand the equations (1.32) to obtain
x = r cos(θ + φ) =r(cos θ cos φ − sin θ sinφ)
y = r sin(θ + φ) =r(sin θ cos φ + cos θ sinφ)
(1.34)
Substitute the results from the equations (1.33) into the equations (1.34) to ob�tain the transformation equations from the rotated coordinates to the unrotated
coordinates. One finds these transformation equations can be expressed
x =¯x cos θ − y¯sin θ
y =¯x sin θ + ¯y cos θ
(1.35)
Solving the equations (1.35) for x¯ and y¯ produces the inverse transformation
x¯ =x cos θ + y sin θ
y¯ = − x sin θ + y cos θ
(1.36)
Inverse Functions
If a function y = f(x) is such that it never takes on the same value twice, then
it is called a one-to-one function. One-to-one functions are such that if x1 �= x2, then
f(x1) �= f(x2). One can test to determine if a function is a one-to-one function by
using the horizontal line test which is as follows. If there exists a horizontal line
y = a constant, which intersects the graph of y = f(x) in more than one point, then
there will exist numbers x1 and x2 such that the height of the curve at x1 is the
same as the height of the curve at x2 or f(x1) = f(x2). This shows that the function
y = f(x) is not a one-to-one function.
Let y = f(x) be a single-valued function of x which is a one-to-one function such as
the function sketched in the figure 1-23(a). On this graph interchange the values of
x and y everywhere to obtain the graph in figure 1-23(b). To represent the function32
x = f(y) with y in terms of x define the inverse operator f−1 with the property that
f−1f(x) = x. Now apply this operator to both sides of the equation x = f(y) to obtain
f−1(x) = f−1f(y) = y or y = f−1(x). The function y = f−1(x) is called the inverse
function associated with the function y = f(x). Rearrange the axes in figure 1-23(b)
so the x-axis is to the right and the y-axis is vertical so that the axes agree with
the axes representation in figure 1-23(a). This produces the figure 1-23(c). Now
place the figure 1-23(c) on top of the original graph of figure 1-23(a) to obtain the
figure 1-23(d), which represents a comparison of the original function and its inverse
function. This figure illustrates the function f(x) and its inverse function f−1(x) are
one-to-one functions which are symmetric about the line y = x.
Figure 1-23. Sketch of a function and its inverse function.
Note that some functions do not have an inverse function. This is usually the
result of the original function not being a one-to-one function. By selecting a domain
of the function where it is a one-to-one function one can define a branch of the function
which has an inverse function associated with it.
Lets examine what has just been done in a slightly different way. If y = f(x) is a
one-to-one function, then the graph of the function y = f(x) is a set of ordered pairs
(x, y), where x ∈ X, the domain of the function and y ∈ Y the range of the function.33
Now if the function f(x) is such that no two ordered pairs have the same second
element, then the function obtained from the set
S = { (x, y) | y = f(x), x ∈ X}
by interchanging the values of x and y is called the inverse function of f and it is
denoted by f−1. Observe that the inverse function has the domain of definition Y
and its range is X and one can write
y = f(x) ⇐⇒ f−1(y) = x (1.32)
Still another way to approach the problem is as follows. Two functions f(x)
and g(x) are said to be inverse functions of one another if f(x) and g(x) have the
properties that
g(f(x)) = x and f(g(x)) = x (1.33)
If g(x) is an inverse function of f(x), the notation f−1, (read f-inverse), is used to
denote the function g. That is, an inverse function of f(x) is denoted f−1(x) and has
the properties
f−1(f(x)) = x and f(f−1(x)) = x (1.34)
Given a function y = f(x), then by interchanging the symbols x and y there results
x = f(y). This is an equation which defines the inverse function. If the equation
x = f(y) can be solved for y in terms of x, to obtain a single valued function, then
this function is called the inverse function of f(x). One then obtains the equivalent
statements
x = f(y) ⇐⇒ y = f−1(x) (1.35)
The process of interchanging x and y in the representation y = f(x) to obtain
x = f(y) implies that geometrically the graphs of f and f−1 are mirror images of
each other about the line y = x. In order that the inverse function be single valued
and one-to-one, it is necessary that there are no horizontal lines, y = constant, which
intersect the graph y = f(x) more than once. Observe that one way to find the inverse
function is the following.34
(1.) Write y = f(x) and then interchange x and y to obtain x = f(y)
(2.) Solve x = f(y) for the variable y to obtain y = f−1(x)
(3.) Note the inverse function f−1(x) sometimes turns out to be a multiple-valued
function. Whenever this happens it is customary to break the function up into
a collection of single-valued functions, called branches, and then one of these
branches is selected to be called the principal branch of the function. That is,
if multiple-valued functions are involved, then select a branch of the function
which is single-valued such that the range of y = f(x) is the domain of f−1(x).
An example of a function and its inverse is given in the figure 1-22.
Figure 1-22. An example of a function and its inverse.
Example 1-6. (Inverse Trigonometric Functions)
The inverse trigonometric functions are defined in the table 1-1. The inverse
trigonometric functions can be graphed by interchanging the axes on the graphs
of the trigonometric functions as illustrated in the figures 1-23 and 1-24. Observe
that these inverse functions are multi-valued functions and consequently one must
define an interval associated with each inverse function such that the inverse function
becomes a single-valued function. This is called selecting a branch of the function
such that it is single-valued.35
Table 1-1
Inverse Trigonometric Functions
Alternate Interval for
Function notation Definition single-valuedness
arcsinx sin−1 x sin−1 x = y if and only if x = sin y −π
2 ≤ y ≤ π
2
arccosx cos−1 x cos−1 x = y if and only if x = cos y 0 ≤ y ≤ π
arctanx tan−1 x tan−1 x = y if and only if x = tan y −π
2 < y < π
2
arccot x cot−1 x cot−1 x = y if and only if x = cot y 0 < y < π
arcsec x sec−1 x sec−1 x = y if and only if x = sec y 0 ≤ y ≤ π, y �= π
2
arccsc x csc−1 x csc−1 x = y if and only if x = csc y −π
2 ≤ y ≤ π
2 , y �= 0

Figure 1-23. The inverse trigonometric functions sin−1 x, cos−1 x and tan−1 x.
There are many different intervals over which each inverse trigonometric function
can be made into a single-valued function. These different intervals are referred to
as branches of the inverse trigonometric functions. Whenever a particular branch is
required for certain problems, then by agreement these branches are called principal
branches and are always used in doing calculations. The following table gives one
way of defining principal value branches for the inverse trigonometric functions.
These branches are highlighted in the figures 1-23 and 1-24.36
Principal Values for Regions Indicated
x < 0 x ≥ 0
−π
2 ≤ sin−1 x < 0 0 ≤ sin−1 x ≤ π
2
π
2 ≤ cos−1 x ≤ π 0 ≤ cos−1 x ≤ π
2
−π
2 ≤ tan−1 x < 0 0 ≤ tan−1 x < π
2
π
2 < cot−1 x < π 0 < cot−1 x ≤ π
2
π
2 ≤ sec−1 x ≤ π 0 ≤ sec−1 x < π
2
−π
2 ≤ csc−1 x < 0 0 < csc−1 x ≤ π
2

Figure 1-24. The inverse trigonometric functions cot−1 x, sec−1 x and csc−1 x.
Equations of lines
Given two points (x1, y1) and (x2, y2) one can plot these points on a rectangular
coordinate system and then draw a straight line � through the two points as illus�trated in the sketch given in the figure 1-25. By definition the slope of the line is
defined as the tangent of the angle α which is formed where the line � intersects the
x-axis.37
Move from point (x1, y1) to point (x2, y2) along the line and let ∆y denote a change
in y and let ∆x denote a change in x, then the slope of the line, call it m, is calculated
slope of line = m = tanα = y2 − y1
x2 − x1
= change in y
change in x = ∆y
∆x (1.36)
If (x, y) is used to denote a variable point which moves along the line, then one can
make use of similar triangles and write either of the statements
m = y − y1
x − x1
or m = y − y2
x − x2
(1.37)
The first equation representing the change in y over a change in x relative to the
first point and the second equation representing a change in y over a change in x
relative to the second point on the line.
This gives the two-point formulas for representing a line
y − y1
x − x1
= y2 − y1
x2 − x1
= m or y − y2
x − x2
= y2 − y1
x2 − x1
= m (1.38)
 hhhhhhh
hhhhhhh
Figure 1-25. The line y − y1 = m(x − x1)
Once the slope m = change in y
change in x
= tanα of the line is known, one can represent
the line using either of the point-slope forms
y − y1 = m(x − x1) or y − y2 = m(x − x2) (1.39)
Note that lines parallel to the x-axis have zero slope and are represented by
equations of the form y = y0 = a constant. For lines which are perpendicular to the
x-axis or parallel to the y-axis, the slope is not defined. This is because the slope38
tends toward a + infinite slope or - infinite slope depending upon how the angle of
intersection α approaches π/2. Lines of this type are represented by an equation
having the form x = x0 = a constant. The figure 1-26 illustrates the general shape
of a straight line which has a positive, zero and negative slope.

Figure 1-26. The slope of a line.
positive slope zero slope negative slope ±∞ slope
The general equation of a line is given by
Ax + By + C = 0, where A, B, C are constants. (1.40)
The slope-intercept form for the equation of a line is given by
y = mx + b (1.41)
where m is the slope and b is the y−intercept. Note that when x = 0, then the point
(0, b) is where the line intersects the y axis. If the line intersects the y-axis at the
point (0, b) and intersects the x-axis at the point (a, 0), then the intercept form for
the equation of a straight line is given by
x
a
+ y
b = 1, a �= 0, b �= 0 (1.42)
One form1 for the parametric equation of a straight line is given by the set of points
� = { (x, y) | x = t and y = mt + b, −∞ < t < ∞ }
Another parametric form such as
� = { (x, y) | x = sin t and y = m sin t + b, −∞ < t < ∞ }
gives only a segment of the total line.
1 The parametric representation of a line or curve is not unique and depends upon the representation.39
The polar form for the equation of a straight line can be obtained from the
intercept form for a line, given by equation (1.42), by using the transformation
equations (1.1) previously considered. For example, if the intercept form of the line
� is x
a
+ y
b = 1, then the transformation equations x = r cos θ and y = r sin θ change this
equation to the form
r cos θ
a
+
r sin θ
b = 1 (1.43)

Figure 1-27. Determining polar form for line.
Let d denote the perpendicular distance
from the line � to the origin of the rectan�gular x, y coordinate system as illustrated
in the figure 1-27. This perpendicular line
makes an angle β such that
cos β = d
a
and cos(π
2 − β) = sin β = d
b
Solve for 1
a
and 1
b and substitute the results
into the equation (1.43) to show
r
d cos θ cos β +
r
d sin θ sin β = 1
Use trigonometry to simplify the above equation and show the polar form for the
equation of the line is
r cos(θ − β) = d (1.44)
Here (r, θ) is a general point in polar coordinates which moves along the line � de�scribed by the polar equation (1.44) and β is the angle that the x-axis makes with
the line which passes through the origin and is perpendicular to the line �.
Perpendicular Lines
Consider a line �2 which is perpendicular to a given line
�1 as illustrated in the figure 1-28. The slope of the line
�1 is given by m1 = tan α1 and the slope of the line �2 is
given by m2 = tan α2 where α1 and α2 are the positive
angles made when the lines �1 and �2 intersect the x-axis.
Figure 1-28. Perpendicular lines.
40
Two lines are said to intersect orthogonally when they intersect to form two right
angles. Note that α2 is an exterior angle to a right triangle ABC and so one can
write α2 = α1 +π/2. If the two lines are perpendicular, then the product of the slopes
m1 and m2 must satisfy
m1m2 = tanα1 tanα2 =
� sinα1
cos α1
� sin(α1 + π/2)
cos(α1 + π/2) = sin α1
cosα1
· cosα1
(− sinα1) = −1 (1.45)
which shows that if the two lines are perpendicular, then the product of their slopes
must equal -1, or alternatively, one slope must be the negative reciprocal of the other
slope. This relation breaks down if one of the lines is parallel to the x-axis, because
then a zero slope occurs.
In general, if line �1 with slope m1 = tan θ1 inter�sects line �2 with slope m2 = tan θ2 and θ denotes the
angle of intersection as measured from line �1 to �2,
then θ = θ2 − θ1 and
tan θ = tan(θ2 − θ1) = tan θ2 − tan θ1
1 + tan θ1 tan θ2
tan θ = m2 − m1
1 + m1m2
Note that as m2 approaches −1/m1, then the angle θ approaches π/2.
Limits
The notation x → ∞ is used to denote the value x increasing without bound
in the positive direction and the notation x → −∞ is used to denote x increasing
without bound in the negative direction.
The limits limx→∞ f(x) and lim x→−∞ f(x), if they
exist, are used to denote the values of a function f(x) as the variable x is allowed
to increase without bound in the positive and negative directions. For example one
can write
limx→∞(2 + 1
x) = 2 and lim x→−∞(2 + 1
x2 ) = 2
The notation x → x0 denotes the variable x approaching the finite value x0, but
it never gets there. If x and x0 denote real numbers, then x can approach x0 from
any direction and get as close to x0 as you desire, but it cannot equal the value x0.
For � > 0 a small real number, sketch on a piece of paper the difference between the
x-values defined by the sets
N = {x | | x − x0| < �} and N0 = {x | 0 < |x − x0| < �} (1.46)41
Observe that the set N contains all the points between x0 − � and x0 + � together with
the point x0 ∈ N, while the set N0 is the same as N but has the point x0 excluded so
one can write x0 ∈/ N0. The set N is called a neighborhood of the point x0 while the set
N0 is called a deleted neighborhood of the point x0. The notation x → x0 emphasizes
the requirement that x approach the value x0, but x is restricted to taking on the
values in the set N0. The situation is illustrated in the figures 1-29(a) and 1-29(b).
The notation x → x+
0 is used to denote x approaching x0 from the right-hand side of
x0, where x is restricted such that x > x0. The notation x → x−
0 is used to denote x
approaching x0 from the left-hand side of x0, where x is restricted such that x < x0.
In general, the notation x → x0 means x can approach x0 from any direction, but x
can never equal x0.

Figure 1-29. Left and right-hand approaches of x to the value x0.
Infinitesimals
You cannot compare two quantities which are completely different in every way.
To measure related quantities you must have
(i) A basic unit of measurement applicable to the quantity being measured.
(ii) A number representing the ratio of the measured quantity to the basic unit.
The concept of largeness or smallness of a quantity is relative to the basic unit
selected for use in the measurement.
For example, if a quantity Q is divided up
into some fractional part f, then fQ is smaller than Q because the ratio fQ/Q = f
is small. For f < 1, quantities like fQ, f 2Q, f 3Q, . . . are called small quantities of
the first, second, third orders of smallness, since each quantity is a small fraction
f of the previous quantity. If the fraction f is allowed to approach zero, then the
quantities fQ, f 2Q, f 3Q, . . . are very, very small and are called infinitesimals of the
first, second, third, . . ., orders. Thus, if ∆x is a small change in x, then (∆x)2 would
be an infinitesimal of the second order, (∆x)3 would be an infinitesimal of the third
order, etc.42
In terms of limits, if α and β are infinitesimals and limα→0
β
α
is some constant
different from zero, then α and β are called infinitesimals of the same order. However,
if limα→0
β
α
= 0, then β is called an infinitesimal of higher order than α.
If you are dealing with an equation involving infinitesimals of different
orders, you only need to retain those infinitesimals of lowest order, since the higher
order infinitesimals are significantly smaller and will not affect the results
when these infinitesimals approach zero .
This concept is often used in comparing the ratio of two small quantities which
approach zero. Consider the problem of finding the volume of a hollow cylinder, as
illustrated in the figure 1-30, as the thickness of the cylinder sides approaches zero.

Figure 1-30. Volume of hollow cylinder.
Let ∆V denote the volume of the hollow cylinder with r the inner radius of the
hollow cylinder and r + ∆r the outer radius. One can write
∆V =Volume of outer cylinder − Volume of inner cylinder
∆V =π(r + ∆r)2h − πr2h = π[r2 + 2r∆r + (∆r)2]h − πr2h
∆V =2πrh∆r + πh(∆r)
2
This relation gives the exact volume of the hollow cylinder. If one takes the limit
as ∆r tends toward zero, then the ∆r and (∆r)2 terms become infinitesimals and
the infinitesimal of the second order can be neglected since one is only interested in
comparison of ratios when dealing with small quantities. For example
lim
∆r→0
∆V
∆r
= lim
∆r→0
(2πrh + πh∆r) = 2πrh43
Limiting Value of a Function
The notation limx→x0
f(x) = � is used to denote the limiting value of a function f(x)
as x approaches the value x0, but x �= x0. Note that the limit statement limx→x0
f(x) is
dependent upon values of f(x) for x near x0, but not for x = x0. One must examine
the values of f(x) both for x+
0 values (values of x slightly greater than x0) and for
x−
0 values (values of x slightly less than x0). These type of limiting statements are
written
lim
x→x+
0
f(x) and lim
x→x−
0
f(x)
and are called right-hand and left-hand limits respectively. There may be situations
where (a) f(x0) is not defined (b) f(x0) is defined but does not equal the limiting
value � (c) the limit limx→x0
f(x) might become unbounded, in which case one can write
a statement stating that “no limit exists as x → x0 ”.
Some limits are easy to calculate, for example lim
x→2
(3x + 1) = 7, is a limit of the
form limx→x0
f(x) = f(x0), where f(x0) is the value of f(x) at x = x0, if the value f(x0)
exists. This method is fine if the graph of the function f(x) is a smooth unbroken
curve in the neighborhood of the point x0.

Figure 1-31. Sectionaly -continuous function
The limiting value limx→x0
f(x) cannot be calculated by eval�uating the function f(x) at the point x0 if the function is
not defined at the point x0. A function f(x) is called a
sectionally continuous function if its graph can be repre�sented by sections of unbroken curves. The function f(x)
defined
f(x) = � 2 − (x − x0), x < x0
5 + 2(x − x0), x > x0
is an example of a sectionally continuous function. Note this function is not defined
at the point x0 and the left-hand limit lim
x→x−
0
f(x) = 2 and the right-hand limit given
by lim
x→x+
0
f(x) = 5 are not equal and f(x0) is not defined. The graph of f(x) is sketched
in the figure 1-31. The function f(x) is said to have a jump discontinuity at the point
x = x0 and one would write limx→x0
f(x) does not exit.
Some limiting values produce the indeterminate forms 0
0 or ∞
∞ and these resulting
forms must be analyzed further to determine their limiting value. For example, the44
limiting value 0
0 may reduce to a zero value, a finite quantity or it may become an
infinite quantity as the following examples illustrate.
limx→0
3x2
2x
= limx→0
3
2
x = 0, a zero limit
limx→0
3x
2x
= limx→0
3
2 = 3
2
, a finite limit
limx→0
3x
2x2 = limx→0
3
2x = ∞, an infinite limit
limx→x0
x2 − x2
0
x − x0
= limx→x0
(x − x0)(x + x0)
(x − x0) = 2x0,
a finite limit
Example 1-7. (Geometry used to determine limiting value)
Consider the function f(x) = sin x
x
and observe that this function is not defined
at the value x = 0, because f(0) = sin x
x x=0
= 0
0
, an indeterminate form.
Let us investigate the limit limx→0
sin x
x using the geometry of the figure 1-32 as the angle2 x
gets very small, but with x �= 0. The figure 1-32 illustrates part of a circle of radius
r sketched in the first quadrant along with a ray from the origin constructed at the
angle x. The lines AD and BC perpendicular to the polar axis are constructed along
with the line BD representing a chord. These constructions are illustrated in the
figure 1-32. From the geometry of figure 1-32 verify the following values.
AD = r sin x
BC = r tan x
Area � 0BD = 1
2
0B · AD = 1
2
r2 sin x
Area sector 0BD = 1
2
r2x
Area � 0BC = 1
2
0B · BC = 1
2
r2 tan x
One can compare the areas of triangles �0BD, �0BC and sector 0BD to come
up with the inequalities
Area � 0BD ≤ Area sector 0BD ≤ Area � 0BC
or
1
2
r2 sin x ≤
1
2
r2x ≤
1
2
r2 tan x
(1.47)
Divide this inequality through by 1
2 r2 sin x to obtain the result 1 ≤
x
sin x
≤
1
cos x
.
Taking the reciprocals one can write
1 ≥
sin x
x
≥ cos x (1.48)
2 Radian measure is always used. 45

Figure 1-32. Construction of triangles and sector associated with circle.
Now take the limit as x approaches zero to show
1 ≥ limx→0
sin x
x
≥ limx→0
cos x (1.49)
The function sin x
x
is squeezed or sandwiched between the values 1 and cos x and since
the cosine function approaches 1 as x approaches zero, one can say the limit of the
function sin x
x
must also approach 1 and so one can write
limx→0
sin x
x
= 1 (1.50)
In our study of calculus other methods are developed to verify the above limiting
value associated with the indeterminate form sin x
x
as x approaches zero.
Example 1-8. (Algebra used to determine limiting value)
Algebra as well as geometry can be used to aid in evaluating limits. For example,
to calculate the limit
limx→1
xn − 1
x − 1 = xn − 1
x − 1 x=1
= 0
0
an indeterminate form (1.51)
one can make the change of variables z = x−1 and express the limit given by equation
(1.51) in the form
lim
z→0
(1 + z)n − 1
z
(1.52)
The numerator of this limit expression can be expanded by using the binomial
theorem
(1 + z)
n = 1 + nz +
n(n − 1)
2! z2 +
n(n − 1)(n − 2)
3! z3 + · · · (1.53)46
Substituting the expansion (1.53) into the equation (1.52) and simplifying reduces
the given limit to the form
lim
z→0
�
n +
n(n − 1)
2! z +
n(n − 1)(n − 2)
3! z2 + · · ·�
= n (1.54)
This shows that limx→1
xn − 1
x − 1 = n
Example 1-9. (Limits)
The following are some examples illustrating limiting values associated with
functions.
limx→3
x2 = 9
lim
x→0+
1
x
= + ∞
lim
x→0−
1
x = − ∞
limx→∞ �
3 + 1
x
�
= 3
lim
θ→0
tan θ
θ = 1
limx→0
√x + 1 − 1
x = 1
2
Formal Definition of Limit
In the early development of mathematics the concept of a limit was very vague.
The calculation of a limit was so fundamental to understanding certain aspects of calculus, that it required a precise definition.
A more formal −δ (read epsilon-delta) definition of a limit was finally developed around the 1800’s.
( https://en.wikipedia.org/wiki/(%CE%B5,_%CE%B4)-definition_of_limit )
This formalization
resulted from the combined research into limits developed by the mathematicians
Weierstrass,3 Bolzano4 and Cauchy. 5
Definition 1: Limit of a function
Let f(x) be defined and single-valued for all values of x in some deleted neigh�borhood of the point x0. A number � is called a limit of f(x) as x approaches x0,
written limx→x0
f(x) = �, if for every small positive number � > 0 there exists a number
δ such that 6
|f(x) − �| < � whenever 0 < |x − x0| < δ (1.55)
Then one can write f(x) → � (f(x) approaches �) as x → x0 (x approaches x0).
Note that f(x) need not be defined at the point x0 in order for a limit to exist.
3 Karl Theodor Wilhelm Weierstrass (1815-1897) A German mathematician.
4 Bernard Placidus Johan Nepomuk Bolzano (1781-1848) A Bohemian philosopher and mathematician.
5 Augustin Louis Cauchy (1789-1857) A French mathematician.
6 The number δ usually depends upon how � is selected.47
The above definition must be modified if restrictions are placed upon how x
approaches x0. For example, the limits lim
x→x+
0
f(x) = �1 and lim
x→x−
0
f(x) = �2 are called
the right-hand and left-hand limits associated with the function f(x) as x approaches
the point x0. Sometimes the right-hand limit is expressed lim
x→x+
0
f(x) = f(x+
0 ) and
the left-hand limit is expressed lim
x→x−
0
f(x) = f(x−
0 ). The � − δ definitions associated
with these left and right-hand limits is exactly the same as given above with the
understanding that for right-hand limits x is restricted to the set of values x > x0
and for left-hand limits x is restricted to the set of values x < x0.
Definition 2: Limit of a function f(x) as x → ∞
Let f(x) be defined over the unbounded interval c < x < ∞, then a number � is
called a limit of f(x) as x increases without bound, written as limx→∞ f(x) = �, if for
every � > 0, there exists a number N1 > 0 such that |f(x) − �| < �, whenever x ≥ N1.
In a similar fashion, if f(x) is defined over the unbounded interval −∞ < x < c,
then the number � is called a limit of f(x) as x decreases without bound, written
lim x→−∞ f(x) = �, if for every � > 0, there exists a number N2 > 0 such that |f(x) − �| < �,
whenever x ≤ −N2.
In terms of the graph { (x, y) | y = f(x), x ∈ R } one can say that for x sufficiently
large, larger than N1 or less than −N2, the y values of the graph would get as close
as you want to the line y = �.
Definition 3: Limit of a function becomes unbounded
In the cases where the limit limx→x0
f(x) either increases or decreases without bound
and does not approach a limit, then the notation limx→x0
f(x) = +∞ is used to denote
that there exists a number N3 > 0, such that f(x) > N3, whenever 0 < |x − x0| < δ and
the notation limx→x0
f(x) = −∞ is used to denote that there exists a number N4 > 0,
such that f(x) < −N4, whenever 0 < |x − x0| < δ.
In the above notations the symbols +∞ (plus infinity) and −∞ (minus infinity)
are used to denote unboundedness of the functions. These symbols are not numbers.
Also observe that there are situations where to use the above notation one might
have to replace the limit subscript x → x0 by either x → x+
0 or x → x−
0 in order to
denote right or left-handed limits.48
In using the � − δ methods to prove limit statements, observe that the statement
“f(x) is near �” is expressed mathematically by the statement |f(x) − �| < � where
� > 0 is very small. By selecting � very small you can force f(x) to be very near �,
but what must δ be in order that f(x) be that close to �? The selection of δ, in most
cases, will depend upon how � is specified. The statement that “x is near x0, but x
is not equal to x0 ” is expressed mathematically by the statement 0 < |x − x0| < δ.
The real number δ which is selected to achieve the smallness specified by �, is not
a unique number. Once one value of δ is found, then any other value δ1 < δ would
also satisfy the definition.
Figure 1-33.
(a) Graphical sketch of � − δ limit.
(b) Function having jump discontinuity at the point x0
A sketch of the � − δ definition of a limit is given in the figure 1-33(a). Here
x0, �, � > 0, δ > 0 are all real numbers and the given function y = f(x) is understood to
be well defined for both x < x0 and for x > x0, while the function value f(x0) may or
may not be defined. That portion of the graph inside the shaded rectangle is given
by the set of values
G = { (x, y) | 0 < |x − x0| < δ and y = f(x) }
which is a subset of all the points inside the shaded rectangle.49
The shaded rectangle consists of the set of values
S = { (x, y) | 0 < |x − x0| < δ and |y − �| < � }
Note that the line where x = x0 and � − � < y < � + � is excluded from the set. The
problem is that for every � > 0 that is specified, one must know how to select the
δ to insure the curve stays within the shaded rectangle. If this can be done then �
is defined to be the limx→x0
f(x). In order to make |f(x) − �| small, as x → x0, one must
restrict the values of x to some small deleted neighborhood of the point x0. If only
points near x0 are to be considered, it is customary to always select δ to be less than
or equal to 1. Thus if |x − x0| < 1, then x is restricted to the interval [x0 − 1, x0 + 1].
Example 1-10. (� − δ proof)
Use the � − δ definition of a limit to prove that lim
x→3
x2 = 9
Solution
Here f(x) = x2 and � = 9 so that
|f(x) − �| = |x2 − 9| = |(x + 3)(x − 3)| = |x + 3| · |x − 3| (1.56)
To make |f(x) − �| small one must control the size of |x− 3|. Recall that by agreement
δ is to be selected such that δ < 1 and as a consequence of this the statement “x is
near 3” is to mean x is restricted to the interval [2, 4]. This information allows us to
place bounds upon the factor (x + 3). That is, |x + 3| < 7, since x is restricted to the
interval [2, 4]. One can now use this information to change equation (1.56) into an
inequality by noting that if |x − 3| < δ, one can then select δ such that
|f(x) − �| = |x2 − 9| = |x + 3| · |x − 3| < 7δ < � (1.57)
where � > 0 and less than 1, is as small as you want it to be. The inequality (1.57)
tells us that if δ < �/7, then it follows that
|x2 − 9| < � whenever |x − 3| < δ
Special Considerations
1. The quantity � used in the definition of a limit is often replaced by some scaled
value of �, such as α �, �2,
√�, etc. in order to make the algebra associated with
some theorem or proof easier.50
2. The limiting process has the property that for f(x) = c, a constant, for all values
of x, then
limx→x0
c = c (1.58)
This is known as the constant function rule for limits.
3. The limiting process has the property that for f(x) = x, then limx→x0
x = x0.
This is sometimes called the identity function rule for limits.
Properties of Limits
If f(x) and g(x) are functions and the limits limx→x0
f(x) = �1 and limx→x0
g(x) = �2 both
exist and are finite, then
(a) The limit of a constant times a function equals the constant times the limit of
the function.
limx→x0
cf(x) = c limx→x0
f(x) = c �1 for all constants c
(b) The limit of a sum is the sum of the limits.
limx→x0
[f(x) + g(x)] = limx→x0
f(x) + limx→x0
g(x) = �1 + �2
(c) The limit of a difference is the difference of the limits.
limx→x0
[f(x) − g(x)] = limx→x0
f(x) − limx→x0
g(x) = �1 − �2
(d) The limit of a product of functions equals the product of the function limits.
limx→x0
[f(x) · g(x)] = �
limx→x0
f(x)
�
·
�
limx→x0
g(x)
�
= �1 · �2
(e) The limit of a quotient is the quotient of the limits provided that the denom�inator limit is nonzero.
limx→x0
f(x)
g(x) =
limx→x0
f(x)
limx→x0
g(x) = �1
�2
, provided �2 �= 0
(f) The limit of an nth root is the nth root of the limit.
limx→x0
�n f(x) = n
� limx→x0
f(x) = √
n
�1
�if n is an odd positive integer or
if n is an even positive integer and �1 > 0
(g) Repeated applications of the product rule with g(x) = f(x) gives the extended
product rule.
limx→x0
f(x)
n =
�
limx→x0
f(x)
�n
(h) The limit theorem for composite functions is as follows.
If limx→x0
g(x) = �, then limx→x0
f(g(x)) = f
�
limx→x0
g(x)
�
= f(�)51
Example 1-11. (Limit Theorem)
Use the � − δ definition of a limit to prove the limit of a sum is the sum of the
limits limx→x0
(f(x) + g(x)) = limx→x0
f(x) + limx→x0
g(x) = �1 + �2
Solution By hypothesis, limx→x0
f(x) = �1 and limx→x0
g(x) = �2, so that for a small number
�1 > 0, there exists numbers δ1 and δ2 such that
|f(x) − �1| < �1 when 0 < |x − x0| < δ1
|g(x) − �2| < �1 when 0 < |x − x0| < δ2
where �1 > 0 is a small quantity to be specified at a later time. Select δ to be the
smaller of δ1 and δ2, then using the triangle inequality, one can write
|(f(x) + g(x)) − (�1 + �2)| =|(f(x) − �1) + (g(x) − �2)|
≤ |f(x) − �1| + |g(x) − �2|
≤ �1 + �1 = 2�1 when 0 < |x − x0| < δ
Consequently, if �1 is selected as �/2, then one can say that
|(f(x) + g(x)) − (�1 + �2)| < � when 0 < |x − x0| < δ
which implies
limx→x0
(f(x) + g(x)) = limx→x0
f(x) + limx→x0
g(x) = �1 + �2
Example 1-12. (Limit Theorem)
Use the � − δ definition of a limit to prove the limit of a product of functions
equals the product of the function limits. That is, if limx→x0
f(x) = �1 and limx→x0
g(x) = �2,
then limx→x0
f(x)g(x) = �
limx→x0
f(x)
� � limx→x0
g(x)
�
= �1�2.
Solution
By hypothesis, limx→x0
f(x) = �1 and limx→x0
g(x) = �2, so that for every small number
�1, there exists numbers �1, δ1 and �1, δ2 such that
|f(x) − �1| < �1, whenever 0 < |x − x0| < δ1
and |g(x) − �2| < �1 whenever 0 < |x − x0| < δ2
where �1 > 0 is some small number to be specified later. Let δ equal the smaller of
the numbers δ1 and δ2 so that one can write
|f(x) − �1| < �1, |g(x) − �2| < �1, whenever 0 < |x − x0| < δ52
To prove the above limit one must specify how to select δ associated with a given
value of � such that
|f(x)g(x) − �1�2| < � whenever |x − x0| < δ
One can select �1 above as a small number which is some scaled version of �. Observe
that the function f(x) is bounded, since by the triangle inequality one can write
|f(x)| = |f(x) − �1 + �1| < |f(x) − �1| + |�1| < �1 + |�1| < 1 + |�1|
where �1 is assumed to be less than unity. Also note that one can write
|f(x)g(x) − �1�2| =|f(x)g(x) − �2f(x) + �2f(x) − �1�2|
≤|f(x)(g(x) − �2)| + |�2(f(x) − �1)|
≤|f(x)||g(x) − �2| + |�2||f(x) − �1|
≤(1 + |�1|)�1 + |�2|�1 = (1 + |�1| + |�2|)�1
Consequently, if the quantity �1 is selected to satisfy the inequality (1+|�1|+|�2|)�1 < �,
then one can say that
|f(x)g(x) − �1�2| < � whenever |x − x0| < δ
so that
limx→x0
f(x)g(x) = �
limx→x0
f(x)
� � limx→x0
g(x)
�
= �1�2
Example 1-13. (Limit Theorem)
If �2 �= 0, prove that if limx→x0
g(x) = �2, then limx→x0
1
g(x) = 1
limx→x0
g(x) = 1
�2
Solution By hypothesis limx→x0
g(x) = �2, with �2 �= 0. This means that for every �1 > 0
there exists a δ1 such that |g(x) − �2| < �1 whenever |x − x0| < δ1. How can this
information be used to show that for every � > 0 there exists a δ such that
�
�
�
�
1
g(x) − 1
�2
�
�
�
�
< � whenever |x − x0| < δ ? (1.59)
The left-hand side of the inequality (1.59) can be expressed
�
�
�
�
1
g(x) − 1
�2
�
�
�
� = |�2 − g(x)|
|g(x)�2| = |g(x) − �2|
|�2| · 1
|g(x)| (1.60)53
For a given �1, one can find a δ1 such that the quantity |g(x) − �2| < �1 whenever
|x − x0| < δ1. What can be constructed as an inequality concerning the quantity
1
|g(x)|
? If �2 �= 0 one can employ the triangle inequality and write
|�2| = |�2 − g(x) + g(x)| ≤ |�2 − g(x)| + |g(x)|
By the definition of a limit, one can select values �3 and δ3 such that
|g(x) − �2| < �3 when |x − x0| < δ3
This gives the inequalities
|�2| < �3 + |g(x)| or |�2| − �3 < |g(x)| or
1
|g(x)|
<
1
|�2| − �3
(1.61)
provided |�2| − �3 is not zero. Recall that the values of �1 and �3 have not been
specified and their values can be selected to have any small values that we desire.
The inequality given by equation (1.60) can be expressed in the form
�
�
�
�
1
g(x) − 1
�2
�
�
�
�
< |g(x) − �2|
|�2| · 1
|g(x)|
<
�1
|�2|
· 1
|�2| − �3
(1.62)
and is valid for all x values satisfying |x− x0| < δ, where δ is selected as the smaller of
the values δ1 and δ3. Let us now specify an �1 and �3 value so that with some algebra
the right-hand side of equation (1.62) can be made less than � for |x − x0| < δ. One
way to accomplish this is as follows. After � is selected, one can select δ1 above to go
with �1 = �(1 − β)|�2|
2 and select δ3 above to go with �3 = β|�2|, where β is some small
fraction less than 1. Then δ is selected as the smaller of the values δ1 and δ3 and the
product on the right-hand side of equation (1.62) is less than � for |x − x0| < δ.
The above result can now be combined with the limit of a product rule
limx→x0
f(x)h(x) = limx→x0
f(x) · limx→x0
h(x) with h(x) = 1
g(x) to establish the quotient rule
limx→x0
f(x)
g(x) =
�
limx→x0
f(x)
� � limx→x0
1
g(x)
�
=
limx→x0
f(x)
limx→x0
g(x) = �1
�2
, provided �2 �= 0
The Squeeze Theorem
Assume that for x near x0 there exists three functions f(x), g(x) and h(x) which
can be shown to satisfy the inequalities f(x) ≤ g(x) ≤ h(x). If one can show that
limx→x0
f(x) = � and limx→x0
h(x) = �,
then one can conclude
limx→x0
g(x) = �
This result is known as the squeeze theorem. 54
Continuous Functions and Discontinuous Functions
A function f(x) is called a continuous function over the interval a ≤ x0 ≤ b if for
all points x0 within the interval
(i) f(x0) is well defined
(ii) limx→x0
f(x) exists
(iii) limx→x0
f(x) = f(x0)
(1.63)
Polynomial functions are continuous functions.
Rational algebraic functions,
represented by the quotient of two polynomials, are continuous except for those
points where the denominator becomes zero. The trigonometric functions, exponen�tial functions and logarithmic functions are continuous functions over appropriate
intervals.
Alternatively, one can assume the right-hand limit lim x→x0+ f(x) = �1 and the left�hand limit lim
x→x−
0
f(x) = �2 both exist, then if �1 = �2 and f(x0) = �1, then the function
f(x) is said to be continuous at the point x0. A function continuous at all points x0
within an interval is said to be continuous over the interval.
If any of the conditions given in equation (1.63) are not met, then f(x) is called
a discontinuous function. For example, if lim x→x0+ f(x) = �1 and lim
x→x−
0
f(x) = �2 both exist
and �1 �= �2, the function f(x) is said to have a jump discontinuity at the point x0.
An example of a function with a jump discontinuity is given in the figure 1-33(b).
If limx→x0
f(x) does not exist, then f(x) is said to be discontinuous at the point x0.
The Intermediate Value Property states that a function f(x) which is continuous
on a closed interval a ≤ x ≤ b is such that when x moves from the point a to the point
b the function takes on every intermediate value between f(a) and f(b) at least once.
An alternative version of the intermediate value property
is the following. If y = f(x) denotes a continuous function
on the interval a ≤ x ≤ b, where f(a) < c < f(b), and the
line y = c = constant is constructed , then the Intermediate
Value Theorem states that there must exist at least one
number ξ satisfying a < ξ < b such that f(ξ) = c.55
Example 1-14. (Discontinuities)
(a) f(x) = x2−1
x−1 is not defined at the point x = 1, so f(x) is said to be discontin�uous at the point x = 1. The limit limx→1
(x − 1)(x + 1)
x − 1
= 2 exists and so by defining
the function f(x) to have the value f(1) = 2, the function can be made continuous.
In this case the function is said to have a removable discontinuity at the point
x = 1.
(b) If limx→x0
f(x) = ±∞, then obviously f(x) is not defined at the point x0. Another
way to spot an infinite discontinuity is to set the denominator of a function equal
to zero and solve for x. For example, if f(x) = 1
(x − 1)(x − 2)(x − 3), then f(x) is
said to have infinite discontinuities at the points x = 1, x = 2 and x = 3.
(c) The function f(x) = � 1, x < 2
5, x > 2 is not defined at the point x = 2. The
left and right-hand limits as x → 2 are not the same and so the function is said
to have a jump discontinuity at the point x = 2. The limit limx→2 f(x) does not
exist. At a point where a jump discontinuity occurs, it is sometimes convenient
to define the value of the function as the average value of the left and right-hand
limits.
Asymptotic Lines
A graph is a set of ordered pairs (x, y) which are well defined over some region
of the x, y-plane. If there exists one or more straight lines such that the graph
approaches one of these lines as x or y increases without bound, then the lines are
called asymptotic lines.
Example 1-15. (Asymptotic Lines)
Consider the curve C = { (x, y) | y = f(x) = 1+ 1
x − 1
, x ∈ R } and observe that the
curve passes through the origin since when x = 0 one finds y = f(0) = 0. Also note
that as x increases, limx→∞ f(x) = 1 and that as x approaches the value 1, limx→1
f(x) = ±∞.
If one plots some selected points one can produce the illustration of the curve C as
given by the figure 1-34. In the figure 1-34 the line y = 1 is a horizontal asymptote
associated with the curve and the line x = 1 is a vertical asymptote associated with
the curve.56
Consider a curve defined by one of the equations
G(x, y) = 0, y = f(x), x = g(y)
If a line � is an asymptotic line associated with one of the above curves, then the
following properties must be satisfied. Let d denote the perpendicular distance from
a point (x, y) on the curve to the line �. If one or more of the conditions
limx→∞ d = 0, lim x→−∞ d = 0, lim
y→∞ d = 0, lim
y→−∞ d = 0,
is satisfied, then the line � is called an asymptotic line or asymptote associated with
the given curve.

Figure 1-34. The graph of y = f(x) = 1 + 1
x − 1
y = 1 +
1
x − 1
y = 1
x = 1
Finding Asymptotic Lines
One can determine an asymptotic line associated with a curve y = f(x) by ap�plying one of the following procedures.
1. Solve for y in terms of x and set the denominator equal to zero and solve for x.
The resulting values for x represent the vertical asymptotic lines.
2. Solve for x in terms of y and set the denominator equal to zero and solve for y.
The resulting values for y represent the horizontal asymptotic lines.
3. The line x = x0 is called a vertical asymptote if one of the following conditions
is true.
limx→x0
f(x) = ∞, lim
x→x−
0
f(x) = ∞, lim
x→x+
0
f(x) = ∞
limx→x0
f(x) = −∞, lim
x→x−
0
f(x) = −∞, lim
x→x+
0
f(x) = −∞57
4. The line y = y0 is called a horizontal asymptote if one of the following condi�tions is true.
limx→∞ f(x) = y0, lim x→−∞ f(x) = y0
5. The line y = mx + b is called a slant asymptote or oblique asymptote if
limx→∞ [f(x) − (mx + b)] = 0
Example 1-16. Asymptotic Lines
Consider the curve y = f(x) = 2x + 1 +
1
x
, where x ∈ R. This function has the
properties that
limx→∞ [f(x) − (2x + 1)] = limx→∞
1
x
= 0 and limx→0
f(x) = ±∞
so that one can say the line y = 2x + 1 is an oblique asymptote and the line x = 0 is
a vertical asymptote. A sketch of this curve is given in the figure 1-35.

Figure 1-35. Sketch of curve y = f(x) = 2x + 1 +
1
x
y = 2x + 1
x = 0
Conic Sections
A general equation of the second degree has the form
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 (1.64)
where A, B, C, D, E, F are constants. All curves which have the form of equation (1.64)
can be obtained by cutting a right circular cone with a plane. The figure 1-36(a)
illustrates a right circular cone obtained by constructing a circle in a horizontal plane
and then moving perpendicular to the plane to a point V above or below the center
of the circle. The point V is called the vertex of the cone. All the lines through the
point V and points on the circumference of the circle are called generators of the58
cone. The set of all generators produces a right circular cone. The figure 1-36(b)
illustrates a horizontal plane intersecting the cone in a circle. The figure 1-36(c)
illustrates a nonhorizontal plane section which cuts two opposite generators. The
resulting curve of intersection is called an ellipse. Figure 1-36(d) illustrates a plane
parallel to a generator of the cone which also intersects the cone. The resulting
curve of intersection is called a parabola. Any plane cutting both the upper and
lower parts of a cone will intersect the cone in a curve called a hyperbola which is
illustrated in the figure 1-36(e).

Figure 1-36. The intersection of right circular cone with a plane.
Conic sections were studied by the early Greeks. Euclid7 supposedly wrote four
books on conic sections. The Greek geometer Appollonius8 wrote eight books on
conic sections which summarized Greek knowledge of conic sections and his work
has survived the passage of time.
Conic sections can be defined as follows. In the xy-plane select a point f, called
the focus, and a line D not through f. This line is called the directrix. The set of
points P satisfying the condition that the distance from f to P, call it r = P f , is some
multiple e times the distance d = PP�, where d represents the perpendicular distance
from the point P to the line D. The resulting equation for the conic section is
obtained from the equation r = e d with the geometric interpretation of this equation
illustrated in the figure 1-37.
7 Euclid of Alexandria (325-265 BCE)
8 Appollonius of Perga (262-190 BCE)59

Figure 1-37. Defining a conic section.
The plane curve resulting from the equation
r = e d is called a conic section with eccentricity
e, focus f and directrix D and if the eccentricity e
satisfies
0 < e < 1, the conic section is an ellipse.
e = 1, the conic section is a parabola.
e > 1, the conic section is a hyperbola.
In addition to the focus and directrix there is associated with each conic section
the following quantities.
The vertex V The vertex V of a conic section is the midpoint of a line from the
focus perpendicular to the directrix.
Axis of symmetry The line through the focus and perpendicular to the directrix
is called an axis of symmetry.
Focal parameter 2p This is the perpendicular distance from the focus to the
directrix, where p is the distance from the focus to the vertex or distance from
vertex to directrix.
Latus rectum 2� This is a chord parallel to a directrix and perpendicular to a
focus which passes between two points on the conic section. The latus rectum
is used as a measure associated with the spread of a conic section. If � is the
semi-latus rectum intersecting the conic section at the point where x = p, one
finds r = � = ed and so it follows that 2� = 2ed.
Circle
A circle is the locus of points (x, y) in a plane equidistant from a fixed point called
the center of the circle. Note that no real locus occurs if the radius r is negative or
imaginary. It has been previously demonstrated how to calculate the equation of a
circle. The figure 1-38 is a summary of these previous results. The circle x2 + y2 = r2
has eccentricity zero and latus rectum of 2r. Parametric equations for the circle
(x − x0)2 + (y − y0)2 = r2, centered at (x0, y0), are
x = x0 + r cost, y = y0 + r sin t, 0 ≤ t ≤ 2π60
When dealing with second degree equations of the form x2 + y2 + αx + βy = γ,
where α, β and γ are constants, it is customary to complete the square on the x and
y terms to obtain
(x2 + αx +
α2
4 ) + (y2 + βy + β2
4 ) = γ +
α2
4 + β2
4 =⇒ (x +
α
2 )
2 + (y + β
2
)
2 = r2
where it is assumed that r2 = γ + α2
4 + β2
4 > 0. This produces the equation of a circle
with radius r which is centered at the point �
−α
2 , −β
2
�
.

Figure 1-38. Circle about origin and circle translated to point (x0, y0)
Parabola
The parabola can be defined as the locus of points (x, y) in a plane, such that
(x, y) moves to remain equidistant from a fixed point (x0, y0) and fixed line �. The fixed
point is called the focus of the parabola and the fixed line is called the directrix of
the parabola. The midpoint of the perpendicular line from the focus to the directrix
is called the vertex of the parabola.
In figure 1-39(b), let the point (0, p) denote the focus of the parabola symmetric
about the y-axis and let the line y = −p denote the directrix of the parabola. If (x, y)
is a general point on the parabola, then
d1 =distance from (x, y) to focus = �x2 + (y − p)2
d2 =distance from (x, y) to directrix = y + p61
If d1 = d2 for all values of x and y, then
�x2 + (y − p)2 = y + p or x2 = 4py, p �= 0 (1.65)
This parabola has its vertex at the origin, an eccentricity of 1, a semi-latus rectum
of length 2p, latus rectum of 2� = 4p and focal parameter of 2p.
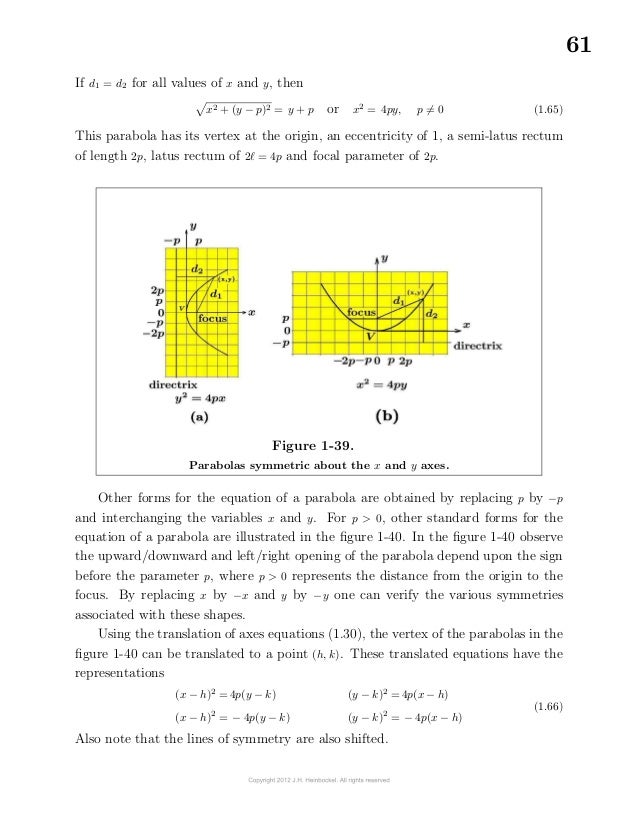
Figure 1-39. Parabolas symmetric about the x and y axes.
Other forms for the equation of a parabola are obtained by replacing p by −p
and interchanging the variables x and y. For p > 0, other standard forms for the
equation of a parabola are illustrated in the figure 1-40. In the figure 1-40 observe
the upward/downward and left/right opening of the parabola depend upon the sign
before the parameter p, where p > 0 represents the distance from the origin to the
focus. By replacing x by −x and y by −y one can verify the various symmetries
associated with these shapes.
Using the translation of axes equations (1.30), the vertex of the parabolas in the
figure 1-40 can be translated to a point (h, k). These translated equations have the
representations
(x − h)2 = 4p(y − k)
(x − h)
2 = − 4p(y − k)
(y − k)2 = 4p(x − h)
(y − k)
2 = − 4p(x − h)
(1.66)
Also note that the lines of symmetry are also shifted.62

Figure 1-40. Other forms for representing a parabola.
One form for the parametric representation of the parabola (x − h)2 = 4p(y − k) is
given by
P = { (x, y) | x = h + t, y = k + t
2/4p, −∞ < t < ∞ } (1.67)
with similar parametric representations for the other parabolas.
Use of determinants
The equation of the parabola passing through the three distinct points (x1, y1),
(x2, y2) and (x3, y3) can be determined by evaluating the determinant9
�
�
�
�
�
�
�
y x2 x 1
y1 x2
1 x1 1
y2 x2
2 x2 1
y3 x2
3 x3 1
�
�
�
�
�
�
�
= 0
provided the following determinants are different from zero.
�
�
�
�
�
�
x2
1 x1 1
x2
2 x2 1
x2
3 x3 1
�
�
�
�
�
�
�= 0, and
�
�
�
�
�
�
x1 y1 1
x2 y2 1
x3 y3 1
�
�
�
�
�
�
�= 0
9 Determinants and their properties are discussed in chapter 10.63
Ellipse
The eccentricity e of an ellipse satisfies 0 < e < 1 so that for any given positive
number a one can state that
ae <
a
e
, 0 < e < 1 (1.68)
Consequently, if the point (ae, 0) is selected as the focus of an ellipse and the line
x = a/e is selected as the directrix of the ellipse, then in relation to this fixed focus
and fixed line a general point (x, y) will satisfy
d1 =distance of (x, y) to focus = �(x − ae)2 + y2
d2 =⊥ distance of (x, y) to directrix = |x − a/e|
The ellipse can then be defined as the set of points (x, y) satisfying the constraint
condition d1 = e d2 which can be expressed as the set of points
E1 = { (x, y) | �(x − ae)2 + y2 = e|x − a/e|, 0 < e < 1 } (1.69)
Applying some algebra to the constraint condition on the points (x, y), the ellipse
can be expressed in a different form. Observe that if d1 = e d2, then
(x − ae)
2 + y2 =e2(x − a/e)
2
or x2 − 2aex + a2e2 + y2 =e2x2 − 2aex + a2
which simplifies to the condition
x2
a2 + y2
a2(1 − e2) = 1 or
x2
a2 + y2
b2 = 1, b2 = a2(1 − e2) (1.70)
where the eccentricity satisfies 0 < e < 1. In the case where the focus is selected as
(−ae, 0) and the directrix is selected as the line x = −a/e, there results the following
situation
d1 =distance of (x, y) to focus = �(x + ae)2 + y2
d2 =⊥ distance of (x, y) to directrix = |x + a/e|64
The condition that d1 = e d2 can be represented as the set of points
E2 = { (x, y) | �(x + ae)2 + y2 = e|x + a/e|, 0 < e < 1 } (1.71)
As an exercise, show that the simplification of the constraint condition for the set
of points E2 also produces the equation (1.70).

Figure 1-41. The ellipse x2
a2 + y2
b2 = 1
Define the constants
c = ae and b2 = a2(1 − e2) = a2 − c2 (1.72)
and note that b2 < a2, then from the above discussion one can conclude that an
ellipse is defined by the equation
x2
a2 + y2
b2 = 1, 0 < e < 1, b2 = a2(1 − e2), c = ae (1.73)
and has the points (ae, 0) and (−ae, 0) as foci and the lines x = −a/e and x = a/e as
directrices. The resulting graph for the ellipse is illustrated in the figure 1-41. This65
ellipse has vertices at (−a, 0) and (a, 0), a latus rectum of length 2b2/a and eccentricity
given by �1 − b2/a2.
In the figure 1-41 a right triangle has been constructed as a mnemonic device to
help remember the relations given by the equations (1.72). The distance 2a between
(−a, 0) and (a, 0) is called the major axis of the ellipse and the distance 2b from (0, −b)
to (0, b) is called the minor axis of the ellipse. The origin (0, 0) is called the center of
the ellipse.

Figure 1-42. Symmetry of the ellipse.
Some algebra can verify the following property satisfied by a general point (x, y)
on the ellipse. Construct the distances
d3 =distance of (x, y) to focus (c, 0) = �(x − c)2 + y2
d4 =distance of (x, y) to focus (−c, 0) = �(x + c)2 + y2
(1.74)
and show
d3 + d4 = �(x − c)2 + y2 + �(x + c)2 + y2 = 2a (1.75)
One can use this property to define the ellipse as the locus of points (x, y) such
that the sum of its distances from two fixed points equals a constant.
The figure 1-42 illustrates that when the roles of x and y are interchanged, then
the major axis and minor axis of the ellipse are reversed. A shifting of the axes so
that the point (x0, y0) is the center of the ellipse produces the equations
(x − x0)2
a2 + (y − y0)2
b2 = 1 or (y − y0)2
a2 + (x − x0)2
b2 = 1 (1.76)
These equations represent the ellipses illustrated in the figure 1-42 where the centers
are shifted to the point (x0, y0).66
The ellipse given by (x − h)2
a2 + (y − k)2
b2 = 1 which is centered at the point (h, k)
can be represented in a parametric form10. One parametric form is to represent the
ellipse as the set of points
E = { (x, y) | x = h + a cos θ, y = k + b sin θ, 0 ≤ θ ≤ 2π } (1.77)
involving the parameter θ which varies from 0 to 2π.
Hyperbola
Let e > 1 denote the eccentricity of a hyperbola. Again let (ae, 0) denote the focus
of the hyperbola and let the line x = a/e denote the directrix of the hyperbola. The
hyperbola is defined such that points (x, y) on the hyperbola satisfy d1 = ed2 where
d1 is the distance from (x, y) to the focus and d2 is the perpendicular distance from
the point (x, y) to the directrix. The hyperbola can then be represented by the set
of points
H1 = { (x, y) |
�(x − ae)2 + y2 = e|x−a/e|, e > 1 }
A simplification of the constraint condition on the set of points (x, y) produces
the alternative representation of the hyperbola
x2
a2 − y2
a2(e2 − 1) = 1, e > 1 (1.78)
Placing the focus at the point (−ae, 0) and using as the directrix the line x = −a/e,
one can verify that the hyperbola is represented by the set of points
H2 = { (x, y) | �(x + ae)2 + y2 = e|x + a/e|, e > 1 }
and it can be verified that the constraint con�dition on the points (x, y) also simplifies to the
equation (1.78).
10 The parametric representation of a curve or part of a curve is not unique.67
Define c = ae and b2 = a2(e2 − 1) = c2 − a2 > 0 and note that for an eccentricity
e > 1 there results the inequality c > a. The hyperbola can then be described as
having the foci (c, 0) and (−c, 0) and directrices x = a/e and x = −a/e. The hyperbola
represented by
x2
a2 − y2
b2 = 1, b2 = a2(e2 − 1) = c2 − a2 (1.79)
is illustrated in the figure 1-43.

Figure 1-43. The hyperbola x2 a2 − y2 b2 = 1
This hyperbola has vertices at (−a, 0) and (a, 0), a latus rectum of length 2b2/a and
eccentricity of �1 + b2/a2. The origin is called the center of the hyperbola. The line
containing the two foci of the hyperbola is called the principal axis of the hyperbola.
Setting y = 0 and solving for x one can determine that the hyperbola intersects
the principal axis at the points (−a, 0) and (a, 0) which are called the vertices of the
hyperbola. The line segment between the vertices is called the major axis of the
hyperbola or transverse axis of the hyperbola. The distance between the points (b, 0)
and (−b, 0) is called the conjugate axis of the hyperbola. The chord through either
focus which is perpendicular to the transverse axis is called a latus rectum. One
can verify that the latus rectum intersects the hyperbola at the points (c, b2/a) and
(c, −b2/a).
Write the equation (1.79) in the form
y = ± b
a
x
�
1 − a2
x2 (1.80)68
and note that for very large values of x the right-hand side of this equation ap�proaches 1. Consequently, for large values of x the equation (1.80) becomes the
lines
y = b
a
x and y = − b
a
x (1.81)
These lines are called the asymptotic lines associated with the hyperbola and are
illustrated in the figure 1-43. Note that the hyperbola has two branches with each
branch approaching the asymptotic lines for large values of x.
Let (x, y) denote a general point on the above hyperbola and construct the dis�tances
d3 =distance from (x, y) to the focus (c, 0) = �(x − c)2 + y2
d4 =distance from (x, y) to the focus (−c, 0) = �(x + c)2 + y2
(1.82)
Use some algebra to verify that
d4 − d3 = 2a (1.83)
This property of the hyperbola is sometimes used to define the hyperbola as the
locus of points (x, y) in the plane such that the difference of its distances from two
fixed points is a constant.
The hyperbola with transverse axis on the x-axis have the asymptotic lines
y = + b
a x and y = − b
a x. Any hyperbola with the property that the conjugate axis has
the same length as the transverse axis is called a rectangular or equilateral hyperbola.
Rectangular hyperbola are such that the asymptotic lines are perpendicular to each
other.

Figure 1-44. Conjugate hyperbola.
69
If two hyperbola are such that the transverse axis of either is the conjugate axis
of the other, then they are called conjugate hyperbola. Conjugate hyperbola will
have the same asymptotic lines. Conjugate hyperbola are illustrated in the figure
1-44.
The figure 1-45 illustrates that when the roles of x and y are interchanged, then
the transverse axis and conjugate axis of the hyperbola are reversed. A shifting
of the axes so that the point (x0, y0) is the center of the hyperbola produces the
equations
(x − x0)2
a2 − (y − y0)2
b2 = 1 or (y − y0)2
a2 − (x − x0)2
b2 = 1 (1.84)
The figure 1-45 illustrates what happens to the hyperbola when the values of x and
y are interchanged.
If the foci are on the x-axis at
(c, 0) and (−c, 0), then x2
a2 − y2
b2 = 1
If the foci are on the y-axis at
(0, c) and (0, −c), then y2
a2 − x2
b2 = 1

Figure 1-45. Symmetry of the hyperbola .
The hyperbola x2
a2 − y2
b2 = 1 can also be represented in a parametric form as the
set of points
H = H1 ∪ H2 where
H1 ={ (x, y) | x = a cosht, y = b sinht, −∞ < t < ∞ }
and H2 ={ (x, y) | x = −a cosht, y = b sinht, −∞ < t < ∞ }
(1.85)
which represents a union of the right-branch and left-branch of the hyperbola. Simi�lar parametric representations can be constructed for those hyperbola which undergo70
a translation or rotation of axes. Remember that the parametric representation of
a curve is not unique.
Conic Sections in Polar Coordinates
Place the origin of the polar coordinate system at the focus of a conic section
with the y-axis parallel to the directrix as illustrated in the figure 1-46. If the point
(x, y) = (r cos θ, r sin θ) is a point on the conic section, then the distance d from the
point (x, y) to the directrix of the conic section is given by either
d = p + r cos θ or d = p − r cos θ (1.86)
depending upon whether the directrix is to the left or right of the focus. The conic
section is defined by r = ed so there results two possible equations r = e(p − r cos θ) or
r = e(p + r cos θ). Solving these equations for r demonstrates that the equations
r = ep
1 − e cos θ or r = ep
1 + e cos θ (1.87)
represent the basic forms associated with representing a conic section in polar coor�dinates.
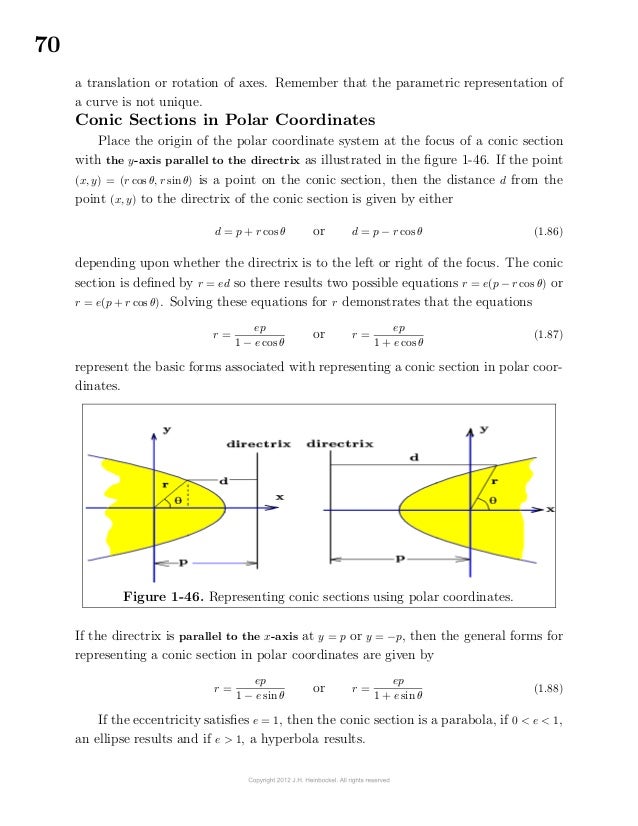
Figure 1-46. Representing conic sections using polar coordinates.
If the directrix is parallel to the x-axis at y = p or y = −p, then the general forms for
representing a conic section in polar coordinates are given by
r = ep
1 − e sin θ or r = ep
1 + e sin θ (1.88)
If the eccentricity satisfies e = 1, then the conic section is a parabola, if 0 < e < 1,
an ellipse results and if e > 1, a hyperbola results. 71
General Equation of the Second Degree
Consider the equation
ax2 + bxy + cy2 + dx + ey + f = 0, (1.89)
where a, b, c, d, e, f are constants, which is a general equation of the second degree. If
one performs a rotation of axes by substituting the rotation equations
x = ¯x cos θ − y¯ sin θ and y = ¯x sin θ + ¯y cos θ (1.90)
into the equation (1.89), one obtains the new equation
a¯x¯2 + ¯bx¯y¯ + ¯cy¯2 + ¯
dx¯ + ¯ey¯ + ¯f = 0 (1.91)
with new coefficients a, ¯ ¯b, ¯c, ¯
d, e, ¯ ¯f defined by the equations
¯a =a cos2 θ + b cos θ sin θ + c sin2 θ
¯b =b(cos2 θ − sin2 θ) + 2(c − a) sin θ cos θ
c¯ =a sin2 θ − b sin θ cos θ + c cos2 θ
¯
d =d cos θ + e sin θ
e¯ = − d sin θ + e cos θ
¯f =f
(1.92)
As an exercise, one can show the quantity b2 − 4ac, called the discriminant, is an
invariant under a rotation of axes. One can show b2−4ac = ¯b2−4¯ac¯. The discriminant is
used to predict the conic section from the equation (1.89). For example, if b2−4ac < 0,
then an ellipse results, if b2 − 4ac = 0, then a parabola results, if b2 − 4ac > 0, then a
hyperbola results.
In the case where the original equation (1.89) has a cross product term xy, so
that b �= 0, then one can always find a rotation angle θ such that in the new equations
(1.91) and (1.92) the term ¯b = 0. If the cross product term ¯b is made zero, then one
can complete the square on the x¯ and y¯ terms which remain. This completing the
square operation converts the new equation (1.90) into one of the standard forms
associated with a conic section. By setting the ¯b term in equation (1.92) equal to
zero one can determine the angle θ such that ¯b vanishes. Using the trigonometric
identities
cos2 θ − sin2 θ = cos 2θ and 2 sin θ cos θ = sin 2θ (1.93)
one can determine the angle θ which makes the cross product term vanish by solving
the equation
¯b = b cos 2θ + (c − a) sin 2θ = 0 (1.94)
for the angle θ. One finds the new term ¯b is zero if θ is selected to satisfy
cot 2θ = a − c
b (recall our hypothesis that b �= 0) (1.95)72
Example 1-17. (Conic Section) Sketch the curve 4xy − 3y2 = 64
Solution
To remove the product term xy from the general equation
ax2 + bxy + cy2 + dx+ ey+ f = 0 of a conic, the axes must be rotated through an angle θ
determined by the equation cot 2θ = a−c
b = 3
4 . For the given conic a = 0, b = 4, c = −3.
This implies that cos 2θ = 3/5 = 1 − 2 sin2 θ or
2 sin2 θ = 2/5 giving sin θ = 1/
√5 and cos θ = 2/
√
5.
The rotation equations (1.90) become
x = 1
√5
(2¯x − y¯) and y = 1
√5
(¯x + 2¯y)
The given equation then becomes
4
�2¯x − y¯ √5
� �x¯ + 2¯y
√5
�
− 3
�x¯ + 2¯y
√5
�2
= 64
which simplifies to the hyperbola x¯2
82 − y¯2
42 = 1 with
respect to the x¯ and y¯ axes.
Example 1-18. The parametric forms for representing conic sections are not
unique. For a, b constants and θ, t used as parameters, the following are some repre�sentative parametric equations which produce conic sections.
Parametric form for conic sections
Conic Section x y parameter
Circle a cos θ a sin θ θ
Parabola at2 2at t
Ellipse a cos θ b sin θ θ
Hyperbola a sec θ b tan θ θ
Rectangular Hyperbola at a/t t
The symbol a > 0 denotes a nonzero constant.
The shape of the curves depends upon the range of values assigned to the pa�rameters representing the curve. Because of this restriction, the parametric repre�sentation usually only gives a portion of the total curve. Sample graphs using the
parameter values indicated are given below.
73
Computer Languages
There are many computer languages and apps that can do graphics and math�ematical computations to aid in the understanding of calculus. Many of these pro�gramming languages can be used to perform specific functions on a computing device
such as a desk-top computer, a lap-top computer, a touch-pad, or hand held calcu�lator. The following is a partial list11 of some computer languages that you might want to investigate. In alphabetical order:
Ada, APL, C, C++, C#, Cobol, Fortran, Java, Javascript, Maple, Mathcad, Math�ematica, Matlab, Pascal, Perl, PHP, Python, Visual Basic.
11
For a more detailed list of programming languages go to: https://en.wikipedia.org/wiki/List_of_programming_languages
Exercises ...
Chapter 2 - Differential Calculus
Chapter two introduces the differential calculus and develops differentiation formulas and rules for finding the derivatives associated with a variety of basic functions.
 hhhhhhh
hhhhhhh
hhhhhhhh
Chapter 3
Chapter three introduces the integral calculus and develops indefinite and definite integrals. Rules for integration and the construction of integral tables are developed throughout the chapter.
Chapter 4
Chapter four is an investigation of sequences and numerical sums and how these quantities are related to the functions, derivatives and integrals of the previous chapters
Chapter 5
Chapter five investigates many selected applications of the differential and integral calculus. The selected applications come mainly from the
areas of economics, physics, biology, chemistry and engineering.
END volume 1
 HHHHHHHHHHHH
HHHHHHHHHHHH
 -
-  ...
...








 (
( <
< 
 < PARTHENON >
< PARTHENON >  , read "the absolute value of x"
, read "the absolute value of x" , read "the cardinality of the
, read "the cardinality of the  , reads "the
, reads "the  , read "the determinant of the
, read "the determinant of the  .
. , denoting the shortest distance between point {\displaystyle P}
, denoting the shortest distance between point {\displaystyle P} to line {\displaystyle ab}
to line {\displaystyle ab} , so line {\displaystyle P|ab}
, so line {\displaystyle P|ab} , read "a divides b" or "a is a factor of b", though Unicode also provides special 'divides' and 'does not divide' symbols (U+2223 and U+2224: ∣, ∤)
, read "a divides b" or "a is a factor of b", though Unicode also provides special 'divides' and 'does not divide' symbols (U+2223 and U+2224: ∣, ∤) , read "f of x, evaluated at x equals 4" (see
, read "f of x, evaluated at x equals 4" (see  , read "the length of the
, read "the length of the  , read "the norm of the (greater-than-one-dimensional) vector {\displaystyle \mathbf {v} }
, read "the norm of the (greater-than-one-dimensional) vector {\displaystyle \mathbf {v} } " (note that absolute value is a one-dimensional norm), although a double vertical bar (see below) is more often used to avoid ambiguity.
" (note that absolute value is a one-dimensional norm), although a double vertical bar (see below) is more often used to avoid ambiguity. , read "the order of the
, read "the order of the  , denoting the restriction of the function {\displaystyle f}
, denoting the restriction of the function {\displaystyle f} , with a domain that is a superset of {\displaystyle A}
, with a domain that is a superset of {\displaystyle A} , to just {\displaystyle A}
, to just {\displaystyle A} , read "the set of x such that x is
, read "the set of x such that x is  , read "f(x) from a to b", denoting {\displaystyle f(b)-f(a)}
, read "f(x) from a to b", denoting {\displaystyle f(b)-f(a)} . Used in the context of a definite integral with variable x.
. Used in the context of a definite integral with variable x.
 , is also employed in mathematics.
, is also employed in mathematics. , read "the line {\displaystyle AB}
, read "the line {\displaystyle AB} is parallel to the line {\displaystyle CD}
is parallel to the line {\displaystyle CD} "
" , read "the norm of the
, read "the norm of the  (read "term {\displaystyle a}
(read "term {\displaystyle a} of type {\displaystyle A}
of type {\displaystyle A}
 reads "
reads " " and {\displaystyle |a|:\left\|A\right\|}
" and {\displaystyle |a|:\left\|A\right\|} ). This has different spacing from
). This has different spacing from  . See below about LaTeX in text mode. ..."
. See below about LaTeX in text mode. ..."
 <
< 
 hhhh
hhhh 

















 hhhhhhh
hhhhhhh



















 hhhhhhh
hhhhhhh